O cabo coaxial. Um cabo coaxial longo é constituído por um cilindro interno condutor de raio e por um cilindro externo coaxial com raio interno e raio externo . O cilindro externo está apoiado em suportes isolantes e não possui nenhuma carga líquida. O cilindro interno possui uma carga por unidade de comprimento uniforme . Determine o campo elétrico em qualquer ponto entre os dois cilindros, a uma distância do eixo; em qualquer ponto no exterior do cilindro. Faça um gráfico do módulo do campo elétrico em função da distância ao eixo do cabo, desde até . Calcule a carga por unidade de comprimento da superfície interna e da superfície externa do cilindro externo.
Passo 1
Supondo uma superfície gaussiana cilíndrica de raio com o mesmo eixo que os cilindros, temos que o seu campo elétrico será dado através da carga por unidade de comprimento que está em seu interior por causa do cilindro interno. Então, usando a equação do campo elétrico para uma linha infinita, teremos:
Que, caso , então o campo elétrico aponta para fora. Caso , ocorre o contrário.
Passo 2
Agora, consideramos uma superfície gaussiana cilíndrica com raio para que esteja externamente a todos os cilindros. Como o cilindro externo não possui nenhuma carga e está apoiado em suportes isolantes, ele está isento de cargas em seu interior e exterior.
Então, a carga da superfície gaussiana será dada pela carga por unidade de comprimento do cilindro interno. Assim, utilizando novamente a equação do campo elétrico para uma linha infinita:
Passo 3
Para construir o gráfico do campo elétrico em função de , temos que determinar o valor do campo em cada intervalo, ou seja, em cada região entre os cilindros.
Com isso, temos que como o cilindro interno é um condutor e está carregado (pela presença de densidade por unidade de comprimento), o campo elétrico em seu interior, ou para , é nulo.
Da mesma forma, no interior do cilindro externo, ou para , não há fluxo elétrico por não haver carga líquida e, por isso, o campo elétrico é nulo.
A partir dessas informações, é possível esboçar o gráfico que queremos:
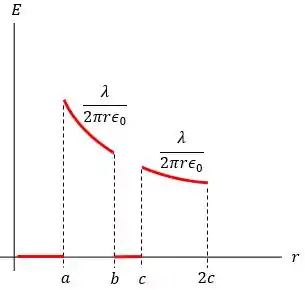
Passo 4
Para calcular a carga por unidade de comprimento da superfície interna do cilindro externo, podemos considerar uma superfície gaussiana cilíndrica que se encontre nessa região, ou seja, tenha raio tal que .
Essa superfície contém em seu exterior a carga do cilindro interno que tem valor e, como o seu campo elétrico é nulo, a carga no seu interior deve ter carga com mesma intensidade e sinal oposto () a fim de anular o campo elétrico na superfície. Portanto, a superfície interna do cilindro externo possui carga por unidade de comprimento .
A partir dessa última conclusão, visto que o cilindro externo tem densidade linear em sua superfície interna, para manter a ausência de campo elétrico, a superfície externa deve ter densidade linear .
Resposta
interno
Externo