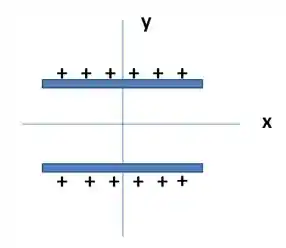
A Fig. 23-43 mostra as seções retas de duas placas de grande extensão, paralelas, não condutoras, positivamente carregadas, ambas com um distribuição superficial de cargas . Determine o campo elétrico , em termos dos vetores unitários,
(a) acima das placas; (b) entre as placas; (c) abaixo das placas.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa situação.
Aqui iremos calcular juntos o resultante do campo elétrico gerado por placas paralelas, em diferentes locais.
Passo 2
- Primeiro, vamos olhar pra região entre as placas e Lembre que o campo elétrico devido a uma placa infinita positivamente carregada aponta para fora dela dessa forma:
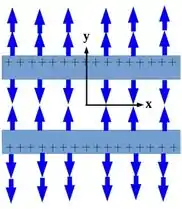
- Nesse caso, como as duas placas estão carregadas positivamente, na região central entre elas os campos de ambas se cancelam, pois estão na mesma direção e sentidos contrários.
- Na região abaixo das duas, o campo é resultado da soma dos campos resultantes de cada placa. Como os dois apontam pra baixo nessa região, então:
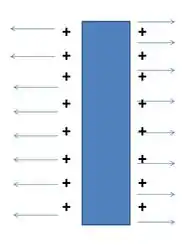
Sendo assim, a gente tem que, na região acima das placas:
Substituindo o valor de do enunciado:
Passo 3
Passo 4
Resposta
- 0 N/C
- -