Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas - Ex. 53
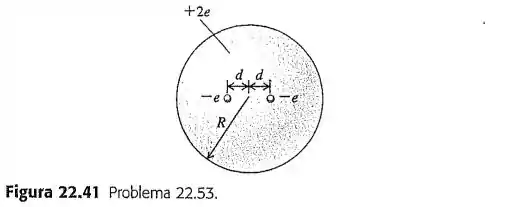
Modelo de Thomson para o átomo, continuação. Usando o modelo (desatualizado) de Thomson para o átomo, descrito no Problema , considere um átomo constituído por dois elétrons, cada um com carga , espalhados no interior de uma esfera de raio , com uma carga total . No equilíbrio, cada elétron está a uma distância do centro do átomo (Figura ). Calcule a distância em termos das outras propriedades do átomo.
Passo 1
Como sabemos, quando se encontram no equilíbrio, os átomos (no caso, os elétrons) não possuem nenhuma força exercendo sobre eles. Isso significa que a força resultante exercida sobre cada um é nula.
Dessa forma, podemos determinar a força agindo sobre um deles, tal que essa força terá mesma intensidade no outro elétron.
Passo 2
Assim, considerando o elétron da esquerda, ele sofre ação de uma força repulsiva causada pelo elétron da direita por ambos serem negativos. Logo, para calcularmos o valor dessa força, temos que usar a Lei de Coulomb que nos dá a força elétrica entre duas cargas puntiformes que estão separados por uma certa distância e tem a forma:
Nesse caso, a força será:
Passo 3
Além disso, o elétron da esquerda (e o da direita também, mas estamos considerando apenas um deles) sofre ação da força atrativa da distribuição de cargas positivas e, lembrando que o campo no interior de uma esfera uniforme carregada é:
Nesse caso, terá o valor de das cargas distribuídas.
E, usando o campo para descobrir o valor da força, usamos:
Passo 4
Portanto, lembrando que a força resultante em cada elétron deve ser nula para a condição de equilíbrio, as forças repulsiva e atrativa no átomo devem ser iguais, tal que:
Que resulta em:
E, logo: