Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.7 - Ex. 30

Uma carga de densidade linear uniforme 2,0   n C / m está distribuída ao longo de uma barra longa, fina, não condutora. A barra está envolvida por uma casca longa, cilíndrica, coaxial, condutora (raio interno: 5,0   c m ; raio externo, 10   c m ). A carga da casca é zero. (a) Determine o módulo do campo elétrico a 15 cm de distância do eixo da casca. Determine a densidade superficial de cargas (b) na superfície interna e (c) na superfície externa da casca.

Passo 1

Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Imagine a situação da questão na figura abaixo:

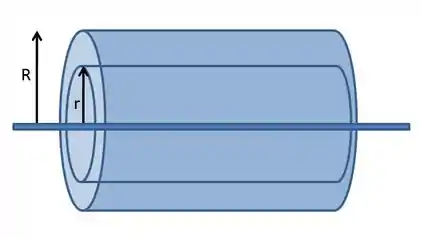
Pra gente calcular o campo elétrico resultante a r =   15   c m de distância do eixo central, basta usarmos a lei de gaus .

Nesse caso, para uma superfície gaussiana que envolve a casca cilíndrica, temos:

∮ A E ⋅ d A = q i n t   ϵ 0

Como a carga interna é devida somente à barra interna e não condutora:

q i n t = q b a r r a = λ L

, sendo λ a densidade linear de carga da barra e L o seu comprimento.

Passo 2

Então:

E ⋅ 2 π r L = λ L ϵ 0  

E = λ 2 π r ϵ 0 = 0,24   k C / N

Passo 3

  1. Uma quantidade de carga igual em módulo e oposta em sinal à carga da barra interna é induzida na superfície da casca interna.

    2. Então, temos que:

    σ i n t e r n a ∙ 2 π ∙ r i n t e r n o ∙ L = - λ ∙ L

    então:

    σ i n t e r n a = - λ 2 π r i n t e r n o = - 6,4   n C / m ²

    Passo 3

  2. Para que o equilíbrio eletrostático seja garantido no cilindro, é necesário que na casca mais externa seja induzida uma carga igual à do passo anterior, mas com sinal contrário.

Nesse caso:

σ e x t e r n a ∙ 2 π ∙ R e x t e r n a ∙ L

= - σ i n t e r n a ∙ 2 π ∙ R i n t e r n a ∙ L

σ e x t e r n a = - σ i n t e r n a ∙ R i n t e r n a R e x t e r n a

= 6,4   n C ∙ 5 10 = 3,2   n C / m ²

Resposta

(a) 0,24   k C / N

(b)   - 6,4 n C m 2

(c)   3,2   n C / m ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma distribuição de cargas não uniforme, mas com simetria esférica, produz um campo elétrico de módulo E=K r 4 , onde K é uma constante e r a distância do centro da esfera. O campo aponta para longe d
A Fig. 23-48 mostra o módulo do campo elétrico do lado de dentro e do lado de fora de uma esfera com uma distribuição uniforme de cargas positivas em função da distância do centro da esfera. A escala
Uma carga pontual produz um fluxo elétrico de -750N· m 2 / C através de uma superfície esférica gaussiana de 10,0c m de raio com centro na carga. (a) Se o raio da superfície gaussiana é multiplicado p
A Fig. 23-53 mostra uma casca esférica com uma densidade volumétrica de cargas uniforme ρ=1,84n C / m 3 , raio interno a=10,0c m e raio externo b=2,00 a . Determine o módulo do campo elétrico (a) em r
Duas cascas esféricas concêntricas carregadas têm raios de 10,0c m e15,0c m . A carga da casca menor é 4,00 ×10 - 8C e a da casca maior é 2,00 × 10 - 8C . Determine o campo elétrico (a) em r=12,0c m ;