A mostra um carro vermelho e um carro verde que se movem um em direção ao outro. A é um gráfico do movimento dos dois carros que mostra suas posições e no instante . O carro vermelho tem uma velocidade constante de e o carro verde parte do repouso. Qual é o módulo da aceleração do carro verde?
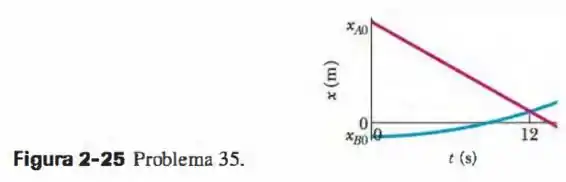

Passo 1
Vamos escrever a equação da posição do carro vermelho como quem não quer nada sabe:
Onde ; (a velocidade é decrescente pois a reta é decrescente) e (esse último pois a equação da posição é uma reta e derivando uma reta duas vezes no tempo nós teremos 0, e a derivada segunda da posição é a aceleração). Portanto:
O que faz sentido pois isso é uma equação de reta. Então para o carro vermelho estará em uma posição igual a:
Essa posição nesse tempo será importantíssima uma vez que os dois carros se encontram nesse tempo.
Passo 2
Agora escrevendo a equação da posição pro carro verde nós teremos:
Onde e já que o carro verde parte do repouso, logo a equação fica:
Em teremos:
Como em os dois carros se encontram então a aceleração do caro verde será de: