Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.7 - Ex. 39

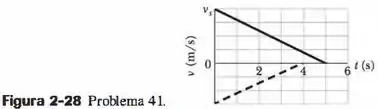
Os maquinistas de dois trens percebem, de repente, que estão em rota de colisão. A Fig. 2 - 28 mostra a velocidade v dos trens em função do tempo t enquanto estão sendo freados. A escala vertical do gráfico é definida por v s = 40,0   m / s . O processo de desaceleração começa quando a distância entre os trens é 200   m . Qual é a distância entre os trens quando, finalmente, conseguem parar?

Passo 1

Pessoal, vamos primeiro tentar retirar todas as informações do gráfico. Podemos notar que há duas retas, cada uma representando a velocidade de cada um dos maquinistas. Vamos chamar de maquinista A o que possui uma reta decrescente e de maquinista B o que possui a reta pontilhada crescente.

Podemos concluir que os dois maquinistas possuem velocidades com sinais opostos, logo eles estão em sentidos diferentes (como diz o enunciado, os trens estão em risco de colidir).

Podemos achar o deslocamento ( Δ s ) através da área do gráfico da velocidade em função do tempo, de modo que

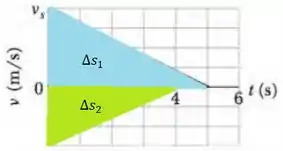
Ou seja, o deslocamento ∆ s 1 é igual a área sob a curva decrescente, enquanto que ∆ s 2 é igual a área da curva crescente. Então partiu calcular esses valores ai...

Passo 2

Deslocamento do maquinista A:

Observando o gráfico temos a velocidade inicial é v 0 = 40   m/s e t = 5   s . A área que corresponde ao Δ s 1   é um triângulo retângulo com catetos iguais a 40 e 5 . Logo:

Δ s 1 = 1 2 ⋅ 5 ⋅ 40

∆ s 1 = 100   m

Isso quer dizer que o trem do maquinista A se deslocou 100   m até parar.

Deslocamento do maquinista B:

Observando o gráfico temos a velocidade inicial é v 0 = - 30   m/s e t = 4   s . A área que corresponde ao Δ s 2   é um triângulo retângulo com catetos iguais a 30 e   4 . Logo:

Δ s 2 = 1 2 ⋅ 4 ⋅ 30

∆ s 2 = 6 0   m

Portanto, temos que o trem do maquinista B se deslocou 60   m até parar.

Dessa maneira, a distância que eles se encontram após pararem, é dada pela diferença do trajeto total de, tal que:

Δ s = 200   m - 60,0   m - 100   m

∆ s = 40,0   m

Resposta

R: 40,0   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula parte da origem em t = 0 e se move no sentido positivo do eixo x . O gráfico da velocidade da partícula em função do tempo é mostrado na Fig. 2-43; a escala vertical é definida por v s =
Um carro que se move com aceleração constante percorreu em 6,00s a distância de 60,0m que separa dois pontos. A velocidade do carro ao passar pelo segundo ponto era 15,0m / s . (a) Qual era a velocida
A distância entre duas estações de metrô é 1100m . Se um trem acelera a + 1,2m / s ² ² a partir do repouso na primeira metade da distância e desacelera a- 1,2m / s ² ² na segunda metade, quais são (a)
Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
(a) Se a aceleração máxima que pode ser tolerada pelos passageiros de um metrô é 1,34m / s 2 e duas estações de metrô estão separadas por uma distância de 806m , qual é a velocidade máxima que o metrô