Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 25.6 - Ex. 50

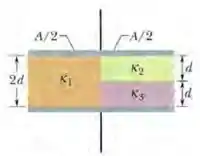
A Fig. 25-49 mostra um capacitor de placas paralelas com uma área das placas A = 10,5 c m 2 e uma distância entre as placas 2 d = 7,12 m m . O lado esquerdo do espaço entre as placas é preenchido por um material de constante dielétrica k 1 = 21,0 ; a parte superior do lado direito é preenchida por um material de constante dielétrica k 2 = 42,0 e a parte inferior do lado direito é preenchida por um material de constante dielétrica k 3 = 58,0 . Qual é a capacitância?

Passo 1

Fala aí! Tudo certinho? Vamos juntar o que fizemos nas questões 48 e 49 desse capítulo. Para descobrir a capacitância desse capacitor dado pela Fig. 25-49.

Nesse problema temos um capacitor cujos dielétricos entre as placas são diferentes e nosso objetivo é determinar a capacitância total do capacitor.

Tem ideia de como fazemos isso? 🤔

Para resolver esse problema vamos separar cada dielétrico em um capacitor e depois fazer a associação de capacitores...

Veja só! 😉

Passo 2

Em primeiro lugar, vamos calcular o lado direito. Temos um capacitor formado por dois dielétricos, κ 2 = 42,0 e κ 3 = 58,0 , colocados um em cima do outro. Para isso, vamos lembrar que nessa configuração eles agem como dois capacitores colocados em série, com distância d ' = d e área A ' = A 2 . A capacitância de cada um é dada por:

C 2 = κ 2 C 0

C 3 = κ 3 C 0

Portanto a capacitância equivalente é

C 23 = C 2 C 3 C 1 + C 2

C 23 = κ 2 C 0 κ 3 C 0 κ 2 C 0 + κ 3 C 0 = C 0 κ 2 κ 3 κ 2 + κ 3

Utilizando a formula para a capacitância de capacitores de placas paralelas:

C 23 = C 0 κ 2 κ 3 κ 2 + κ 3 = ε 0 A / 2 d κ 2 κ 3 κ 2 + κ 3

C 23 = ε 0 A 2 d κ 2 κ 3 κ 2 + κ 3

Tranquilo até aqui? 😎

Passo 3

Para calcular a capacitância do capacitor 1 com constante dielétrica κ 1 = 21,0 , área A ' = A / 2 e distância d ' = 2 d :

C 1 = κ 1 C 0 = κ 1 ε 0 A / 2 2 d

C 1 = κ 1 C 0 = κ 1 ε 0 A 4 d

Dessa forma, para calcular a capacitância total, devemos notar que o dielétrico 1 esta posto de forma que podemos considerar que ele esta formando um capacitor em paralelo com os dielétricos 2 e 3, portanto:

C = C 1 + C 23

C = κ 1 ε 0 A 4 d + ε 0 A 2 d κ 2 κ 3 κ 2 + κ 3 = ε 0 A 2 d κ 1 2 + κ 2 κ 3 κ 2 + κ 3

C = 8,85 × 10 - 12 10,5 × 10 - 4 7,12 × 10 - 3 21,0 2 + 42,0 58,0 42,0 + 58,0

C = 4,55 × 10 - 11 F

E aí! O que achou? Responde Aí! 😉

Resposta

C = 45,5 p F

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um capacitor de 12μ F é conectado a uma fonte de energia que mantém constante uma diferença de potencial de 24V através das placas. Um pedaço de material com constante dielétrica de 3,75 é colocado en
Quando um capacitor de 360n F , imerso no ar, está conectado a uma fonte de tensão, a energia acumulada no capacitor é igual a 1,85 ⋅ 10 - 5J . Mantendo o capacitor conectado à fonte de tensão, inseri
Um capacitor com placas paralelas possui capacitância C = 12,5p F , quando o volume entre as placas é preenchido com ar. As placas são circulares e possuem raio de 3c m . O capacitor é conectado a uma
Um capacitor com placas paralelas possui placas com área de 0,0225m 2 , separadas por 1m m de teflon. a)Calcule a carga nas placas, quando são carregadas a uma diferença de potencial de 12V b)Use a le
Exercício de Livro