Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 25.4 - Ex. 27

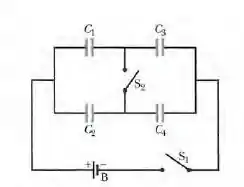
Fig. Abaixo mostra uma bateria de e quatro capacitores descarregados de capacitâncias , , e . Se apenas a chave SI é fechada, determine a carga (a) do capacitor 1; (b) do capacitar 2; (c) do capacitor 3; (d) do capacitar 4. Se as duas chaves são fechadas, determine a carga (e) do capacitar l; (f) do capacitor 2; (g) do capacitor 3; (h) do capacitar 4.

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui temos a situação onde o circuito que temos muda de acordo com o fechamento das chaves.

Passo 2

Item (a)

Na figura abaixo temos o circuito com a chave fechada:

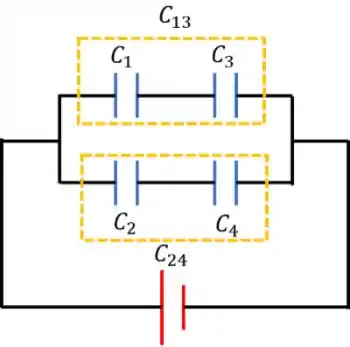
Com a chave fechada, os capacitores 1 e 3 estão em série, e portanto suas cargas são iguais:

Item (b)

Como os capacitores 2 e 4 também estão em série,

Passo 3

Item (c)

Passo 4

Item (d)

Passo 5

Item (e)

Quando a chave 2 é fechada, a diferença de potencial entre os terminais de se torna igual à diferença de potencial entre os terminais de e é dada por:

Então,

Item (f)

Item (g)

Item (h)

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que é possível substituir o sistema de capacitores da figura por um único capacitor equivalente netre os ponstos a e b e calcule a capacitância deste capacitor.

Circuitos que envolvem capacitores nem sempre podem ser agrupados em série e em pararelo. Como por exemplo, a Figura 24.39a mostra três capacitores, C x , C y e C z , formando uma ligação delta, assim

Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica

A figura mostra quatro capacitores, cujo dielétrico é o ar, ligados em um circuito que faz parte de um circuito maior. O gráfico abaixo do circuito mostra o potencial elétrico V(x) em função da posiçã

Na Fig. 25-30, a bateria tem uma diferença de potencial V = 10,0 V e os cinco capacitores têm uma capacitância de 10,0 μF. Determine a carga (a) do capacitor 1; (b) do capacitor 2.