Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.7 - Ex. 31
Na Fig. 27-44, a corrente na resistência 6 é e as resistências são , , e . Qual é a força eletromotriz da fonte ideal?
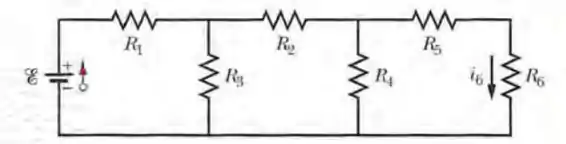
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui deveremos encontrar a fem da fonte ideal a partir da análise do circuito.
Passo 2
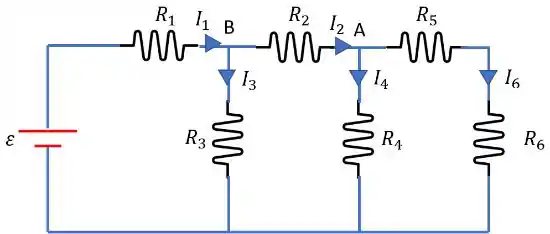
Note que , a queda de tensão em , é a soma das quedas de tensão em e :
Isso significa que a corrente em é dada por . De acordo com a regra dos nós, a corrente em é:
e, portanto, a queda de tensão em é
Passo 3
De acordo com a regra das malhas, a queda de tensão em é
e, portanto, a corrente em é .
Assim, de acordo com a regra dos nós, a corrente em é
,o que significa que a queda de tensão em é
e, portanto, de acordo com a regra das malhas,
Resposta
a)
Exercícios de Livros Relacionados
Na Fig. 27-36, R 1 = R 2 = 4,00 Ω e R 3 = 2,50 Ω . Determine a resistência equivalente entre os pontos D e E. (Sugestão: imagine que existe uma fonte ligada entre os dois pontos.)
Quatro resistores de 18,0 Ω são ligados em paralelo a uma fonte ideal de 25,0 V. Qual é a corrente na fonte?
Descarga lateral. A Fig. 27-38 ilustra uma das razões pelas quais é perigoso se abrigar debaixo de uma árvore durante uma tempestade elétrica. Se um relâmpago atinge a árvore, parte da descarga pode p
Nove fios de cobre de comprimento A e diâmetro d são ligados em paralelo para formar um cabo de resistência R . Qual deve ser o diâmetro D de um fio de cobre de comprimento A ' para que a resistência
A Fig. 27-39 mostra cinco resistores de 5,00 Ω . Determine a resistência equivalente (a) entre os pontos F e H ; (b) entre os pontos F e G . (Sugestão: para cada par de pontos, imagine que existe uma