Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.7 - Ex. 42
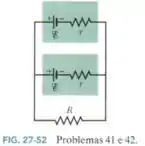
Duas fontes iguais de força eletromotriz e resistencia interna podem ser ligadas a uma resistência em paralelo (Fig. 27-52) ou em série (Fig. 27-53). Se , qual é a corrente na resistência (a) no caso da ligação em paralelo (b) no caso da ligação em série? (c) Em que tipo de ligação a corrente é maior? Se , qual é a corrente na resistência (d) no caso da ligação em paralelo; (e) no caso da ligação em série? (f) Em que tipo de ligação a corrente é maior?
Passo 1
Fala aí! tudo certinho? 😁
Nesse problema temos dois circuitos, um deles temos duas fontes em paralelo com uma resistência e no outro temos duas fontes em série com uma resistência.
Foi dito que cada fonte possui e resistência interna .
A partir daí queremos obter a corrente no resistor em ambos os casos, se e tambem se .
Tem ideia de como fazemos isso? 👀
Para o caso do circuito em paralelo, podemos aplicar o teorema da superposição onde basicamente desligamos uma fonte de cada vez, calculamos a corrente no resistor e no fim somamos os resultados...
Já no caso das fontes em serie, podemos fazer uma associação entre elas, somando o potencial de cada uma e a resistência interna...
Veja só! 😉
Passo 2
Quando a ligação está em paralelo a corrente, , nas fontes é igual. E portanto a corrente no resistor, . Assim, vamos utilizar a lei das malhas para calcular a corrente:
Portanto,
Se , e , então
Tranquilo até aqui? 👀
Passo 3
(b) No caso em que as fontes estão postas em série, todas as resistências estão em série e o valor das fem se soma, portanto:
Substituindo os valores...
(c) Comparando os itens (a) e (b), vemos que na ligação em série a corrente é maior justamente porque as tensões das fontes foram somadas...
Pela lei de Ohm
Se permanece constante e aumenta, para satisfazer a igualdade deve aumentar...
Legal, né?
Passo 4
(d) Temos que a corrente para a ligação em paralelo é:
Mas agora , ou seja
Bem alto, né? 👀
Passo 5
(e) Temos que a corrente para a ligação em série é:
Substituindo os valores...
(f) Comparando os itens (d) e (e), vemos que a ligação em paralelo maior valor de corrente.
Isso porque se analisarmos a lei de Ohm
Embora tenha aumentado no caso em série a resistência interna é maior que a resistência e como no caso das fontes em série se somou, a resistência equivalente do circuito foi maior...
Entendeu tudo? Responde Aí!
Resposta
(a)
(b)
(c) Em série.
(d)
(e)
(f) Em paralelo.