Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.7 - Ex. 39

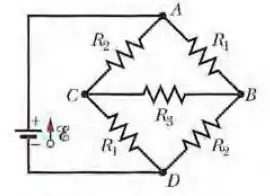
Na Fig. 27-46, ε = 12,0 V , R 1 = 2000 Ω , R 2 = 3000 Ω e R 3 = 4000 Ω . Determine as diferenças de potencial (a) V A - V B ; (b) V B - V C (c) V C - V D ; (d) V A - V C .

Passo 1

Olá, meu amigo. Yuri aqui e estamos buscando aqui calcular a diferença de potencial em diferentes pontos do circuito.

Primeiramente, como o circuito é simétrico temos que as correntes em cima dos dois resistores R 1 vão ser i 1 e o mesmo acontece com os resistores R 2 com correntes i 2 .

Passo 2

Vamos desenhar um circuito análogo ao 27-46 e desenhar a direção das correntes nele.

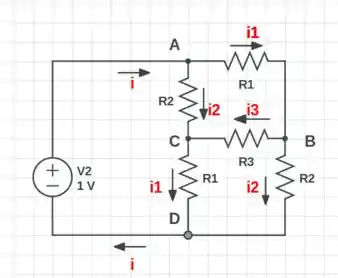
Olhando para o ponto C, vemos que as correntes i 2 e i 3 se unem e sai a corrente i 1 , dessa forma:

i 2 + i 3 = i 1 → i 3 = i 1 - i 2

Agora vamos utilizar a lei das malhas percorrendo primeiramente o caminho ABD:

ε – i 1 R 1 – i 2 R 2 = 0

Colocando a corrente i 2 em evidência:

i 2 = ε - i 1 R 1 R 2

Também, vamos percorrer a malha no caminho ABCD:

ε - i 1 R 1 - i 3 R 3 - i 1 R 1 = 0

ε - 2 i 1 R 1 - i 1 - i 2 R 3 = 0

Substituindo i 2 :

ε - 2 i 1 R 1 - i 1 R 3 + ε - i 1 R 1 R 2 R 3 = 0

Colocando i 1 em evidência:

i 1 R 1 R 3 R 2 + 2 R 1 + R 3 = ε 1 + R 3 R 2

i 1 = ε 1 + R 3 R 2 R 1 R 3 R 2 + 2 R 1 + R 3 - 1

Passo 3

i 1 = 12,0 4000 + 3000 2000 4000 + 2 2000 3000 + 4000 3000 = 2,62 × 10 - 3 A

Dessa forma,

i 2 = ε - i 1 R 1 R 2

também podemos calcular a corrente i 3 = 2,62 × 10 - 3 – 2,25 × 10 - 3 = 0,375 × 10 - 3 A .

Passo 4

(a) A DDP V A – V B é a DDP em cima do resistor 1.

V A – V B = i 1 R 1

V A – V B = 2,62 × 10 - 3 2000 = 5,24 V

Passo 5

(b) A DDP V B – V C é a DDP em cima do resistor 3.

V B – V C = i 3 R 3

V B – V C = 0,375 × 10 - 3 4000 = 1,50 V

Passo 6

(c) A DDP V C – V D é a DDP em cima do resistor 1.

V C – V D = 2,62 × 10 - 3 2000 = 5,24 V

Passo 7

(d) A DDP V A – V C é a DDP em cima do resistor 2.

V A – V C = i 2 R 2

V A – V C = 2,25 × 10 - 3 3000 = 6,75 V

Resposta

(a) V A – V B = 5,24 V

(b) V B – V C = 1,50 V

(c) V C – V D = 5,24 V

(d) V A – V C = 6,75 V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Pretende-se obter uma resistência total de 3,00 Ω ligando uma resistência de valor desconhecido a uma resistência de 12,0 Ω . (a) Qual deve ser o valor da resistência desconhecida? (b) As duas resistê
Na Fig. 27-40, R 1 = 6,00 Ω , R 2 = 18,0 Ω e a força eletromotriz da fonte ideal é E = 12,0 V . Determine (a) o valor absoluto e (b) o sentido (para a esquerda ou para a direita) da corrente i 1 . (c)
Na Fig. 27-41, as fontes ideais têm forças eletromotrizes E 1 = 10,0 V e E 2 = 0,500 E 1 e todas as resistências são de 4,00 Ω . Determine a corrente (a) na resistência 2; (b) na resistência 3.
A Fig. 27-31 mostra uma fonte ligada a um resistor uniforme R 0 . Um contato deslizante pode se deslocar ao longo do resistor do ponto x = 0 , à esquerda, até o ponto x = 10 c m , à direita. O valor d
Na Fig. 27-35 , R 1 = 100 Ω , R 2 = 50 Ω e as fontes ideais têm forças eletromotrizes ε 1 = 6,0 V , ε 2 = 5,0 V e ε 3 = 4,0 V . Determine (a) a corrente no resistor 1; (b) a corrente no resistor 2; (