Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.4 - Ex. 8

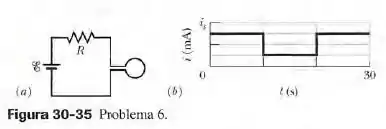
A figura 30-35a mostra um circuito formado por uma fonte ideal de força eletromotriz ε = 6,00   μ V , uma resistência R e uma pequena espira com 5,0   c m ² de área. Um cmapo magnético externo é aplicado à espira durante o intervalo de t = 10   s a t = 20   s . O campo é uniforme, dirigido para dentro do papel na figura 30-35a e o módulo do campo é dado por B = a t , onde B está em teslas, a é uma constante e t está em segundos. A figura 30-35b mostra a corrente i no circuito antes, durante e depois da aplicação do campo. A escala vertical é definida por i = 2,0   m A . Determine o valor da constante a na equação do módulo do campo.

Passo 1

Bom, galera, um cara chamado Faraday descobriu que uma força eletrmotriz e uma corrente podem ser induzidas em uma espira fazendo variar a quantidade de campo magnético que atravessa a espira. Ele ainda percebeu que a dita “quantidade de campo magnético” pode ser visualizada em termos das linhas de campo magnético que atravessam a espira.

O número de linhas que atravessam a espira não importa; os valores da força eletromotriz e da corrente induzida são determinados pela taxa de variação desse número. O módulo da força eletromotriz induzida em uam espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para caluclar a força eletromotriz é a seguinte:

ε = - d ϕ B d t

O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.

De acordo com com o gráfico 30-35b, temos que a corrente é i = 1,5   m A quando t = 0   s e não temos campo aplicado, pois B = a ⋅ 0 = 0   T . Com essas informações, podemos calular a resistência do circuito:

R = ε i = 6,00 × 10 - 6   V 1,5 × 10 - 3   A

R = 0,004   o h m s

Passo 2

Vamos agora olhar para o intervalo 10 < t < 20   s . Para essa situação nós temos o seguinte:

( V f o n t e + ε i n d u z i d a ) R = 0,00050   A

ε i n d u z i d a = 0,0005   A R - V f o n t e

ε i n d u z i d a = 0,0005   A 0,0040 - 6,0 × 10 - 6   V

ε i n d u z i d a = - 4,0 × 10 - 6   V  

Passo 3

Tendo agora em mãos a força eletromotriz induzida, a área da espira e o campo magnético, podemos usar a lei de Faraday para encontrarmos quando vale a constante a ! Vamos substituir na expressão:

ε i n d u z i d a = - d ϕ B d t = - A d B d t = - A d a t d t

ε i n d u z i d a = - A a

a = - ε i n d u z i d a A = 4,0 × 10 - 6   V 5,0 × 10 - 4   m 2

a = 8,0 × 10 - 3   T / s

Resposta

A constante a é igual a:

a = 8,0 × 10 - 3   T / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura 30-42, uma espira circular com 10c m de diâmetro (vista de perfil) é posicionada com a normal N → fazendo um ângulo θ = 30 ° com a direção de um campo magnético uniforme B → cujo módulo e 0,
Um material condutor elástico é esticado e usado para fazer uma espira circular com 12,0c m de raio, que é submetida a um campo magnético uniforme de 0,800T perpendicular ao plano da espira. Ao ser li
Na figura 30-36, o fluxo do campo amgnético na espira aumenta de aordo com a equação ϕ B = 6,0 t 2 + 7,0 t , onde ϕ B está em miliwebers e t em segundos. (a) Qual é o módulo da força eletromotri induz
Uma espira com 12c m de raio e uma resistência de 8,5o h m s é submetida a um campo magnético uniforme B → cujo módulo varia de acorco com a figura 30-33. A escala do eixo vertical é definida por B S
Na figura 30-39, uma bobina de 120 espiras, com 1,8c m de raio e uma resistência de 5,3o h m s , é coaxial com um solenoide de 220e s p i r a s / c m e 3,2c m de diâmetro. A corrente no solenoide dimi