Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.6 - Ex. 14

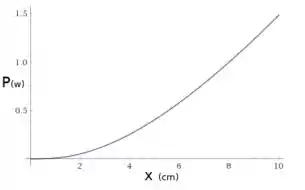
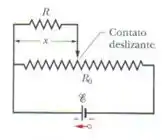
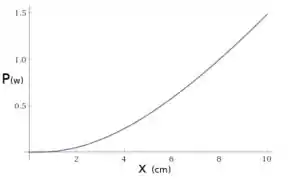
A Fig. 27-31 mostra uma fonte ligada a um resistor uniforme R 0 . Um contato deslizante pode se deslocar ao longo do resistor do ponto x = 0 , à esquerda, até o ponto x = 10 c m , à direita. O valor da resistência à esquerda e à direita do contato depende da posição do contato. Determine a potência dissipada no resistor R em função de x . Plote a função para ε = 50 V , R = 2000 Ω e R 0 = 100 Ω

Passo 1

Fala aí! tudo certinho? 😬

A Figura 27-31 mostra uma fonte de energia elétrica ε conectada a um resistor uniforme R 0 .

Um contato deslizante pode se mover ao longo do resistor, começando no ponto x = 0 (à esquerda) e indo até o ponto x = 10   c m (à direita).

Queremos determinar a potência dissipada no resistor R em função da posição x do contato.

Sabemos que a resistência depende diretamente do comprimento do resistor, portanto, podemos escrever as seguintes funções para a resistência:

R e x = R 0 x 10

R d x = R 0 ( 10 - x ) 10

Onde x é onde o contato se encontra em cm e R e x é a resistência a esquerda do contato e R d x é a resistência a direita. É importante notar que a resistência R esta ligada em paralelo com a resistência R e x e essas duas estão ligadas em série a resistência R d x .

Veja só! 👀

Passo 2

Portanto, vamos calcular a resistência equivalente das que estão ligadas em paralelo:

R e q = R R e x R + R e x

Temos que a corrente que passa pela f e m é:

i = ε R e q + R d

Assim, a diferença de potencial em cima dos resistores ligados em paralelo é

V p = i R e q

V p = ε R e q R e q + R d = ε R R e R + R e R + R e R R e + R d R + R d R e

V p = ε R R e R R e + R d R + R d R e

Agora, para achar a potência dissipada no resistor R :

P R = V p 2 R = 1 R ε R R e R R e + R d R + R d R e 2

Substituindo os valores, temos:

P R =   1 R ε   R R 0 x 10 R R 0 x 10 + R 0 10 - x 10 R + R 0 2 10 - x x 100 2

P R = ε x R 0 2 100 R 100 R R 0 + 10 x – x 2 2

Para os valores de ε = 50 V , R = 2000 Ω e R 0 = 100 Ω , o gráfico é:

E aí! entendeu tudo? Responde Aí! 😎

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada um dos três resistores indicados na Figura 26.62 possui uma resistência de 2,4Ω e pode consumir uma potencia máxima de 36 W sem se tornar excessivamente quente. Qual é a potencia máxima que o cir
No circuito indicado na Figura 26.64, um resistor de 20,0Ω está inserido em um grande bloco de gelo 0,0 ° C , e a bateria possui resistência interna desprezível. Qual é a taxa (em g/s) em que esse cir
62- Qual deve ser o valor da fem ϵ indicada na Figura 26.66 para que a corrente que passa no resistor de 7.0Ω seja igual a 1.80A ?Cada fonte de fem possui resistência interna desprezível.
64- ( a ) Calcule a corrente que passa em cada resistor e na bateria do circuito indicado na Figura 26.68 ( b ) Qual é a resistência equivalente do circuito?
67- No circuito indicado na Figura 26.71 , a corrente que passa pela bateria de 12.0V é medida em 70.6m A no sentido indicado. Qual é a voltagem nos terminais V a b da bateria de 24.0V ?