Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.7 - Ex. 35

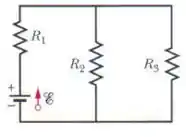
Na Fig. 27-46, R 1 = 2,00 Ω , R 2 = 5,00 Ω e a fonte é ideal. Qual é o valor de R 3 que maximiza a potência dissipada na resistência 3 ?

Passo 1

Fala aí! tudo certinho? 😎

Nesse problema temos um circuito resistivo com os resistores R 2 e R 3 em paralelo e R 1 em série com a equivalente de R 2 e R 3 e nosso objetivo é obter o valor de R 3 de modo que a potência dissipada seja maximizada.

Tem ideia de como fazer isso? 😁

Primeiramente, vamos calcular a resistência equivalente dos resistores R 3 e R 2 :

R 32 = R 3 R 2 R 3 + R 2

Com isso, podemos calcular a DDP em cima do resistor R 3 :

V 3 = i R 32 = i R 3 R 2 R 3 + R 2

Bora começar! 😉

Passo 2

Podemos calcular a corrente na fonte como

i = ε R 1 + R 3 R 2 R 3 + R 2 = ε R 3 + R 2 R 1 R 3 + R 2 + R 3 R 2

Portanto, se V 3 = i R 3 R 2 R 3 + R 2 , então

V 3 = ε R 3 + R 2 R 1 R 3 + R 2 + R 3 R 2 R 3 R 2 R 3 + R 2 = ε R 3 R 2 R 3 R 1 + R 2 + R 1 R 2

Portanto, para calcular a potência, em R 3 :

P 3 = V 3 2 R 3

P 3 = i R 3 R 2 R 3 + R 2 2 1 R 3 = R 3 i R 2 R 3 + R 2 2

Para maximizar a potência, vamos tratar a potência como uma função de R 3 , dessa forma, para achar o máximo basta derivar a potência e igualar a zero:

d P 3 d R 3 = 0

Pela regra do produto, temos

d P 3 d R 3 = i R 2 R 3 + R 2 2 - 2 i R 2 2 R 3 + R 2 3 = 0

ε R 2 R 3 R 1 + R 2 + R 1 R 2 2 = 2 R 3 ε R 2 2 R 1 + R 2 R 3 R 1 + R 2 + R 1 R 2 3

R 3 R 1 + R 2 + R 1 R 2 = 2 R 3 R 1 + R 2

Isolando R 3 , temos

R 3 = R 1 R 2 R 1 + R 2

Substituindo R 1 e R 2

R 3 = 2,00 5,00 2,00 + 5,00 = 1,43 Ω

Sacou? Responde Aí! 😉

Resposta

R 3 = 1,43 Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas lâmpadas, uma de resistência R1, e a outra de resistência R2, R 1R 2 , são ligadas a uma bateria (a) em paralelo e (b) em série. Qual lâmpada é mais brilhante em cada caso?
Na Fig. 29-8 determine a diferença de potencial V d-V c entre os pontos d e c se E1 = 4,0 V, E2 = 1,0 V, R 1 ,=R 2=10 Ω , R3 = 5,0 Ω e a fonte é ideal.
Uma linha de força de 120 V é protegida por um fusível de 15 A. Qual é o número máximo de lâmpadas de 500 W que podem operar, simultaneamente, em paralelo, nessa linha sem “queimar” o fusível?
No circuito da Fig. 29-35, E tem um valor constante mas R pode variar. Determine o valor de R que resulta no aquecimento máximo daquele resistor. A bateria é ideal.
A Fig. 29-37 mostra uma bateria ligada a um resistor uniforme R0. Um contato deslizante pode percorrer o resistor desde x = 0, à esquerda, até v = 10 cm, à direita. Determine uma expressão para a potê