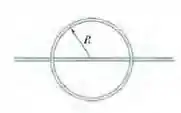
Na figura 30-40, um fio forma uma espira circular de raio e uma resistência de . Um fio retilíneo longo passa pelo centro da espira; no instante , a corrente no fio é , para a direita. Para , a corrente varia de acordo com a equação . (Como o fio é isolado, não há contato entre o fio e a espira.) Qual é o valor absoluto da corrente induzida na espira para ?
Passo 1
E aí, galerinha! 😉

Nesse problema temos um fio que forma uma espira circular de raio e uma resistência de . Um fio retilíneo longo passa pelo centro da espira; no instante , a corrente no fio é , para a direita. Para , a corrente varia de acordo com a equação . A partir daí queremos saber qual é o valor absoluto da corrente induzida na espira para .
Tem ideia de como fazemos isso? 🤔
Bom, galera, um cara chamado Faraday descobriu que uma força eletrmotriz e uma corrente podem ser induzidas em uma espira fazeno variar a quantidade de campo magnético que atravessa a espira. Ele ainda percebeu que a dita “quantidade de campo magnético” pode ser visualizada em termos das linhas de campo magnético que atravessam a espira.
O número de linhas que atravessam a espira não importa; os valores da força eletromotriz e da corrente induzida são determinados pela taxa de variação desse número. O módulo da força eletromotriz induzida em uam espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para caluclar a força eletromotriz é a seguinte:
O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.
Veja só! 😊
Passo 2
Vambora entender o que está acontecendo nessa questão. O fio que passa pelo centro da espira conduz uma corrente que gera um campo magnético na vizinhança dele. Se usarmos a regra da mão direita, veremos que na parte de cima do fio, o campo está saindo do papel e na parte de baixo ele está entrando no papel.
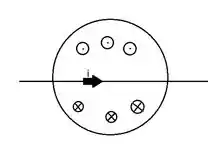
Como queremos saber a corrente induzida na espira, precisamos avaliar o campo magnético que está atravessando a espira. Nesse caso, o total de fluxo através da espira é igual a zero. Logo, como não há variação de fluxo, não há força eletromotriz e, por consequência, não temos corrente induzida.
Sacou? Responde Aí! 👀
Resposta
A corrente é igual a: