Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.4 - Ex. 7

Na Fig. 28-31, um elétron acelerado a partir do repouso por uma diferença de potencial entra no espaço entre duas placas paralelas, separadas por uma distância , entre as quais existe uma diferença de potencial . A placa inferior está a um potencial menor. Despreze o efeito de borda e suponha que o vetor velocidade do elétron é perpendicular ao vetor campo elétrico na região entre as placas. Em termos dos vetores unitários, qual é o valor do campo magnético uniforme para o qual a trajetória do elétron na região entre as placas é retilínea?

Passo 1

Fala aí, pessoal!! Como vai? 😉

Temos primeiramente, um elétron que é acelerado por uma DDP de e então entra em uma região entre placas paralelas, separados por , com um DDP de . Através dessa informação sobre o potencial das placas, podemos definir um esquema considerando a força elétrica causada pelo campo elétrico das placas:

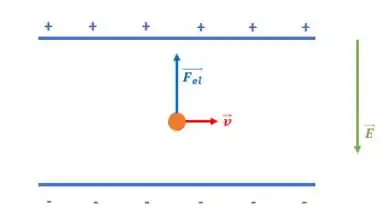
Uma vez que a força elétrica é dada pela multiplicação entre a carga e o campo elétrico :

Podemos entender o sentido da força elétrica ser contrária ao campo elétrico, pois a carga do elétron é negativa!

Como a trajetória é retilínea, as forças elétrica e magnética agindo sobre o elétron se anulam:

Logo podemos então representar a força magnética da seguinte forma:

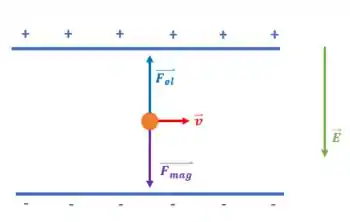
Sabemos que a força nesse caso é dada por:

Passo 2

Vamos reescrever a equação anterior e simplificar:

Dividindo os dois lados pelo valor da carga do elétron:

Como a direção da velocidade é perpendicular ao campo magnético, :

Passo 3

Devemos conservar a energia do elétron, ele nos diz que inicialmente o elétron é acelerado através de uma diferença de potencial, ou seja, a energia é dada pela multiplicação entre o módulo da carga e a diferença de potencial :

Nesse caso, como a carga é um elétron e a DDP é , podemos substituir a equação por:

Enquanto depois, quando o elétron se move entre as placas, temos a energia cinética (não confunde com campo elétrico) em função da massa do elétron e a velocidade do elétron :

Para garantir a conservação de energia do elétron:

Igualando as equações e isolando

Tranquilo até aqui? 😉

Passo 4

E para o campo elétrico, temos que o gradiente do potencial elétrico entre as placas é igual a integral do campo elétrico através do caminho :

Se integrarmos isso pelo caminho entre as duas placas e substituirmos o gradiente do potencial elétrico pela diferença de potencial entre as duas placas , encontraremos: