Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.6 - Ex. 28
Na Fig. 28-38, uma partícula carregada penetra em uma região onde existe um campo magnético uniforme , descreve uma semicircunferência e deixa a região. A partícula, que pode ser um próton ou um elétron (a identidade da partícula faz parte do problema), passa 130 ns na região. (a) Qual é o módulo de ? (b) Se a partícula é enviada de volta para a região onde existe campo magnético com uma energia duas vezes maior, quanto tempo passa na região?
Passo 1
Temos essa partícula que entra em uma região do espaço com um campo magnético e descreve uma semicircunferência e sai da região.
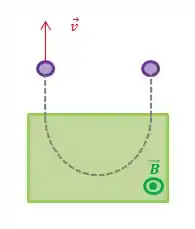
Primeiramente, vamos analisar a figura. A partícula descreve a trajetória no sentido horário e o campo magnético aponta para fora do papel.
Lembrando que a nossa força magnética é dada por , a regra da mão direita aplicada a uma carga que está descendo (assim que entra na região com campo magnético), com a força magnética apontando para fora do plano é:
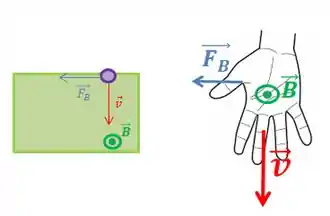
Com a força magnética nessa direção, teríamos o movimento circular como o descrito no desenho, por conta disso, nossa carga é positiva, ela vai receber a força magnética dada pela regra da mão direita e podemos dizer que ela é um próton.
Passo 2
(a) Como a força magnética faz papel de força centrípeta podemos escrever:
Como a velocidade em uma volta é dada pelo comprimento da circunferência divido pelo período (tempo para dar uma volta completa)...
Temos que
Colocando o nosso campo magnético em evidência, teremos que:
No caso desse exercício a partícula dá meia volta, mas por definição, o período é o tempo para dar uma volta completa. Por isso, podemos dizer que o período seria o dobro do tempo que a partícula deu meia volta:
Já a massa e carga do próton são
O nosso campo fica
Passo 3
(b) Voltando para a nossa expressão do campo magnético:
Percebemos que o período não depende da velocidade da partícula. Caso ela fosse enviada com mais energia, essa energia seria a energia cinética e representaria um aumento em sua velocidade, no entanto a velocidade da partícula não varia o período que ela permanece na região.
Sendo assim, o tempoque ela ficará na região, será o mesmo que aquele que foi dado no enunciado para a situação inicial.
Resposta
(a)(b)