Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.Problemas Adicionais - Ex. 94
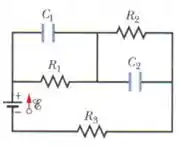
Na Fig. 27-80, , , , , e a fonte ideal tem uma força eletromotriz . Supondo que o circuito se encontra no regime estacionário, qual é a energia total armazenada nos dois capacitores?
Passo 1
E aí, pessoal! 👀
Aqui temos um exercício em que um circuito com dois capacitores e três resistências são organizados de uma forma específica. Como, no regime estacionário, a corrente nos capacitores é zero, a corrente é a mesma nos três resistores.
E agora? o que temos que fazer? 🤔
Podemos aplicar a lei das malhas que diz que em uma malha fechada, o somatório das tensões é igual a zero...
Veja só! 😊
Passo 2
De acordo com a regra das malhas,
Substituindo , , e
temos
Isso significa que a queda de tensão em é
que é também a tensão entre os terminais do capacitor .
De acordo com a Eq. 25-22, a energia armazenada no capacitor é
A queda de tensão em é
que é também a tensão entre os terminais do capacitor . Assim,
A energia total armazenada nos capacitores é
E aí! o que achou? Responde Aí! 😉
