Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Problemas - Ex. 59
Uma barra metálica uniforme, de 458 g e 75,0 cm de comprimento, transporta uma corrente em um campo magnético horizontal uniforme de , como indica a Figura 27.59. A barra está presa por uma dobradiça no ponto b, mas repousa sem estar conectada ao ponto a. Qual é o valor máximo da corrente que pode fluir de a para b, sem romper o contato elétrico no ponto a?
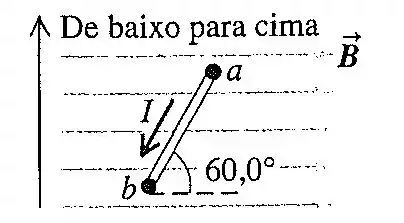
Passo 1
A barra precisa ficar em equilíbrio e por ser um corpo extenso precisamos usar a relação que o torque resultante precisa ser zero.
Passo 2
Na barra só tem duas forças atuando, a força peso e força magnética, ou seja:
Sabemos que , Então temos:
Passo 3
Como queremos a corrente, iremos isolar o .
Resposta
Exercícios de Livros Relacionados
A Fig. 28-46, uma bobina retangular percorrida por corrente e tá no plano de um campo magnético uniforme de módulo 0,040 T . A bobina é formada por uma única espira de fio flexível enrolado em um supo
Um elétron se move em uma circunferência de raio r = 5,29 × 10 - 11 m com uma velocidade de 2,19 × 10 6 m / s . Trate a trajetória circular como uma espira percorrida por uma corrente constante igual
A Fig. 28-45 mostra um cilindro de madeira de massa m = 0,250 k g e comprimento L = 0,100 m , com N = 10,0 espiras de fio enroladas longitudinalmente para formar uma bobina; o plano da bobina passa pe
A Fig. 28-44 mostra uma bobina retangular de cobre, de 20 espiras, com 10 c m de altura e 5 c m de largura. A bobina conduz uma corrente de 0,10 A e dispõe de uma dobradiça em um dos lados verticais.
Um fio situado no eixo y, entre y = 0 e y = 0,250 m , é percorrido por uma corrente de 2,00 m A no sentido negativo do eixo. Na região existe um campo magnético não uniforme dado por B → = 0,300 T / m