Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Exercício - Ex. 35
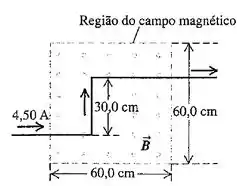
Um fio longo que transporta uma corrente de 4,50 A faz duas dobras 90°, como indica a Figura 27.49. A parte dobrada do fio atravessa um campo magnético uniforme de 0,240 , orientado como indica a figura e confinado a uma região limitada no espaço. Determine o módulo, a direção e o sentido da força que o campo magnético exerce sobre o fio.
Passo 1
Para um fio retilíneo podemos escrever a força magnética como sendo:
Como o fio tem diferentes direções, podemos considerar a força em cada segmento do fio e depois calcular a resultante entre elas.
Passo 2
Vamos chamar de a força magnética no primeiro segmento do fio.
Passo 3
Vamos chamar de a força magnética no segundo segmento do fio.
Passo 4
Vamos chamar de a força magnética no terceiro segmento do fio.
Note que e estão na mesma direção, então podemos somar os dois.
Passo 5
A força resultante será então:
O módulo dessa força será:
Passo 6
A direção será dada pelo ângulo entre as projeções. Então podemos calcular da seguinte forma:
Resposta
,