Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Exercício - Ex. 33
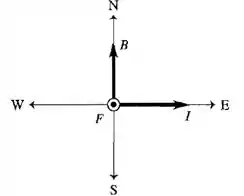
Um fio retilíneo de 2,0 m e 150 g transporta uma corrente em uma região em que o campo magnético da terra é horizontal com um módulo de 0,55 gauss. (a) Qual é o valor mínimo da corrente nesse fio para que seu peso seja totalmente sustentado pela força magnética em função do campo terrestre, supondo que nenhuma outra força, além da gravidade, atue sobre ele? É provável que um fio como esse seja capaz de suportar esse tamanho de corrente? (b) Mostre como o fio teria de ser orientado em relação ao campo magnético da terra para ser sustentado dessa forma.
Passo 1
letra a)
Para a força magnética sustentar o fio, ela precisa ser igual a força peso.
Para um fio teremos:
Como queremos a corrente:
A corrente é muito grande. Então o aquecimento do fio devido a dissipação de energia seria bem severa.
Logo, não é provável que suporte essa corrente.
Passo 2
letra b)
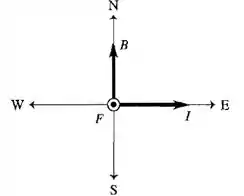
A corrente do fio precisa ter uma direção perpendicular ao campo elétrico e a força magnética, que tem mesma direção e sentido oposto a força peso.
Então podemos desenhar como:
Resposta
letra a), Não é provável.
letra b)
