Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.9 - Ex. 47
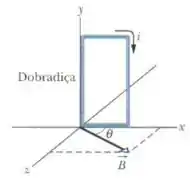
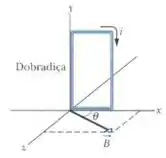
A Fig. 28-47 mostra uma bobina retangular de cobre, de espiras, com de altura e de largura. A bobina conduz uma corrente de e dispõe de uma dobradiça em um dos lados verticais. Está montada no plano , fazendo um ângulo com a direção de um campo magnético uniforme de módulo . Em termos dos vetores unitários, qual é o torque em relação à dobradiça que o campo exerce sobre a bobina?
Passo 1
Fala aí! tudo certinho? 😊
Aqui temos uma bobina quadrada que é feita de várias espiras (fios enrolados) e por esses fios passa uma certa corrente, esta bobina está em um campo magnético que faz um ângulo com a bobina.
Show de bola.
Precisamos aqui calcular o torque gerado sobre essa bobina.
Para isso, temos a seguinte relação:
Onde é o vetor torque, é o momento magnético dipolar dessa bobina e é o campo magnético que atua sobre essa bobina.
Para calcularmos esse torque, precisamos agora saber o momento magnético dipolar da nossa bobina.
Bora lá! 😉
Passo 2
O momento magnético dipolar de uma bobina, tem a seguinte expressão:
Onde são o número de espiras (voltas) que essa bobina tem, é o valor da corrente que passa por ela e é o vetor área dessa bobina.
Mas se liga!
Esse vetor área, tem como módulo a área da bobina.
E a direção e sentido?
A direção e sentido para variar vai ser dada pela regra da mão direita.
Nós vamos pegar a nossa mão direita, e fazer os nossos quatro dedos abraçarem a bobina na direção da corrente, fechamos nossa mão e para onde o nosso polegar apontar, será a direção desse vetor área.
Fazendo isso teremos:
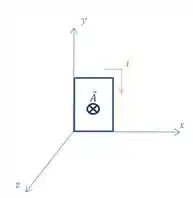
Ou seja, o nosso vetor área aponta na direção negativa do eixo . Escrevendo-o em vetores unitários:
Agora, podemos encontrar o nosso momento magnético dipolar...
Tranquilo até aqui? 😁
Passo 3
Como temos o nosso momento magnético dipolar, agora é só encontrar o nosso torque!
Sendo que o módulo de um produto vetorial é dado por:
E esse ângulo aí...
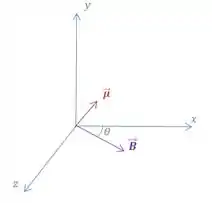
Pela figura, vemos que esse ângulo vai ser
E assim, encontramos o nosso módulo do torque!
E aí, acabou? Não né, a questão nos pediu o torque em vetores unitários... então precisamos fazer a famosa regra da mão direita...
Colocando nossos quatro dedos na direção do momento magnético e nossa palma da mão na direção do campo magnético, vemos que nosso polegar aponta para baixo, por isso o nosso torque está na direção do eixo negativo. Sendo assim, nosso torque em vetores unitários será:
Terminamos mais uma! O que achou? Responde Aí! 👀
