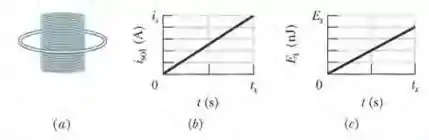
Na Fig. 30-55a, uma espira circular é concêntrica com um solenoide e está em um plano perpendicular ao eixo central do solenoide. A espira tem de raio. O solenoide tem um raio de , possui e a corrente varia com tempo da forma indicada na Fig. 30-55b, onde a escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . A Fig. 30-55c mostra, em função do tempo, a energia que é transforma em energia térmica na espira; a escala no eixo vertical é definida por . Qual a resistência da espira?

Fala aí! como vai? 😁

Nesse problema temos uma espira circular é concêntrica com um solenoide e está em um plano perpendicular ao eixo central do solenoide. A espira tem de raio. O solenoide tem um raio de , possui e a corrente varia com tempo da forma indicada, onde a escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . A figura do enunciado mostra, em função do tempo, a energia que é transforma em energia térmica na espira; a escala no eixo vertical é definida por . A partir daí queremos saber qual a resistência da espira.

Parece complicado? 🤔

A corrente variável que passa pelo solenoide vai induzir, sobre a espira, uma corrente. O mecanismo pelo qual isso acontece é a Lei de Faraday. A questão pede a resistência da espira circular baseada nos gráficos da corrente do solenoide e da energia dissipada como função do tempo.

Para resolver esse problema, o primeiro passo é calcular o fluxo do campo criado pelo solenoide sobre a espira. O campo de um solenoide é

onde é o número de espiras por unidade de comprimento. Como esse campo é restrito apenas à região interna ao solenoide, o fluxo desse campo sobre a espira será

onde é raio do solenoide (não o da espira). Olha que curioso: mesmo calculando o fluxo sobre a espira, só precisamos considerar a área do solenoide, pois apenas através dela teremos fluxo magnético!

Veja só! 😊