Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.6 - Ex. 36
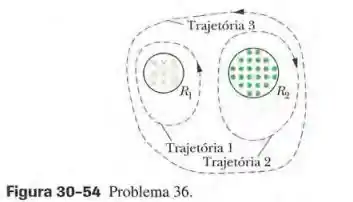
A Fig. 30-54 mostra duas regiões circulares, e , de raios e . Em existe um campo magnético uniforme de módulo dirigido para dentro do papel e em existe um campo magnético uniforme de módulo dirigido para fora do papel (ignore os efeitos de borda). Os dois campos estão diminuindo à taxa de . Calcule o valor (a) para a trajetória 1; (b) para a trajetória 2; (c) para a trajetória 3.
Passo 1
Essa é uma questão que usa a lei de Faraday na forma integral: a integral de linha do campo elétrica sobre um circuito fechado se relaciona com a variação do fluxo magnético sobre a região limitada por esse circuito:
Assim, basta considerarmos variação do fluxo no tempo que termos a integral pedida.
No item (a) vamos focar na trajetória 1. Como o circuito é percorrido no sentido anti-horário, vamos convencionar a normal para fora da folha. Como o campo aponta para dentro, o fluxo será negativo:
Assim,
Como foi dito que o campo diminui a uma taxa constante, temos que
Assim, com , temos que
Passo 2
Para o item (b) vamos focar na trajetória 2 (horária), de modo que vamos convencionar a normal para dentro da folha. Como o campo é para fora, o fluxo será negativo:
Portanto,
Analogamente, temos que
Assim,
Passo 3
Por fim, considerando o a trajetória 3 (anti-horária) com normal para fora da folha:
Assim,
Portanto,