Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 30.9 - Ex. 54

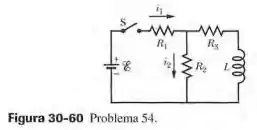
Na Fig. 30-60, E = 100   V , R 1 = 10,0   Ω , R 2 = 20,0   Ω , R 3 = 30,0   Ω e L = 2,00   H . Determine os valores de (a) i 1 e (b) i 2 logo depois que a chave S é fechada. (Considere as correntes nos sentidos indicados na figura como positivas e as correntes no sentido oposto como negativas.) Determine também os valores de (c) i 1 e (d) i 2 muito tempo depois de a chave ter sido fechada. A chave é aberta depois de ter permanecido fechada por muito tempo. Determine os valores de (e) i 1 e (f) i 2 logo depois de a chave ter sido novamente aberta. Determine também os valores de (g) i 1 e (h) i 2 muito tempo depois de a chave ter sido novamente aberta.

Passo 1

Nos itens (a) e (b) temos que considerar o instante imediatamente depois da chave ser aberta e a corrente circular no circuito. Como o indutor está descarregado, a corrente que passa por ele é nula. Com isso, nessa situação podemos desconsiderar totalmente o ramo do circuito que contém o resistor R 3 e o indutor L .

Assim, resta um circuito em série com os resistores R 1 e R 2 . Além disso, a corrente deve ser a mesma:

i 1 = i 2 = i

Aí é só usar a lei de Ohm:

E = R 1 + R 2   i ⇒ i = E R 1 + R 2

Substituindo os valores:

i = 100 10,0 + 20,0 ⇒ i 1 = i 2 = 3,33   A

Passo 2

Agora vamos passar aos itens (c) e (d) em que estamos considerando uma situação muito depois da chave ter sido fechada.

Sabemos que a tensão no indutor é dada por

V i n d = L d i d t

Considerando um tempo muito longo após a chave ser fechada, a tendência é a corrente se estabilizar num regime estacionário, de modo que

d i d t = 0

Com isso, a tensão no indutor é nula, mas a corrente i 3 = i 1 - i 2 que passa por ele e pelo resistor R 3 não é nula.

Para resolver esse problema, temos que usar a lei das malhas. Olhando para a primeira malha:

R 1 i 1 + R 2 i 2 = E

Já na segunda malha:

R 3 i 3 + V i n d - R 2 i 2 = 0

Vimos que V i n d = 0 e i 3 = i 1 - i 2 , de modo que

R 1 i 1 + R 2 i 2 = E R 3 i 1 - i 2 - R 2 i 2 = 0

Substituindo os valores:

10 i 1 + 20 i 2 = 100 30 i 1 - 30 i 2 - 20 i 2 = 0 ⇒ i 1 + 2 i 2 = 10 3 i 1 = 5 i 2

Isolando i 1 na primeira equação:

i 1 = 10 - 2 i 2

Substituindo na segunda equação:

3 10 - 2 i 2 = 5 i 2

30 - 6 i 2 = 5 i 2

i 2 = 30 11 = 2,73   A

Logo,

i 1 = 10 - 2 ⋅ 2,73 = 4,55   A

Portanto, achamos

i 1 = 4,55   A               e           i 2 = 2,73   A

Note que a corrente no indutor é

i 3 = i 1 - i 2 = 4,55 - 2,73 = 1,82   A

Passo 3

Agora vamos aos itens (e) e (f). Depois de muito tempo aberta, a chave será fechada.

Bom, como chave é fechada, a corrente i 1 no resistor R 1 cessa imediatamente, de modo que i 1 = 0   A .

Além disso, após a abertura da chave a corrente do indutor não pode variar bruscamente de modo que ela deve se manter sendo

i 3 = 1,82   A

Olhando agora para a malha fechada da esquerda, a corrente que circula nela deve ser igual em todos os pontos e no sentido horário, de modo que

i 2 = - i 3 = - 1,82   A

Isso significa que a corrente no resistor R 2 é para cima para que a corrente na malha esteja no sentido horário já que ela é a única corrente que circula pelo circuito com a chave aberta.

Passo 4

Por fim, vamos aos itens (g) e (h). Muito tempo após a chave ter sido aberta, como não há alimentação da fonte externa, as correntes todas vão cessar:

i 1 = i 2 = 0   A

Resposta

a   e   b                 i 1 = i 2 = 3,33   A

c   e   d               i 1 = 4,55   A               e           i 2 = 2,73   A

e   e   f             i 1 = 0   A           e           i 2 = - 1,82   A

g   e     h             i 1 = i 2 = 0   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

68 . Você está estudando um solenoide com resistência e indutância desconhecidas. Você o conecta em série com um resistor de 50,0Ω , uma bateria de 25,0V com resistência interna desprezível e uma chav
52 . Um indutor com indutância L = 0,200H e resistência desprezível está ligado a uma bateria, uma chave S e dois resistores, R 1 = 8,00Ω e R 2 = 6,00Ω (Figura P 30.52 ). A bateria tem emf de 48,0V e
65 . No circuito indicado na Figura P 30.65 , a chave S é fechada no instante t = 0 . ( a ) Determine a leitura de cada instrumento logo após a chave S ser fechada. ( b ) Qual é a leituraapós a chave
50 . Um indutor com indutância L = 0,300H e resistência desprezível está ligado a uma bateria, uma chave S e dois resistores, R 1 = 12,0V e R 2 = 16,0V (Figura P 30.50 ). A bateria tem fem de 96,0V e
QUENCHING EM UM ÍMÃ DE R M . Ímãs transportando correntes muito grandes são usados para produzir os campos magnéticos uniformes e intensos necessários para os exames por ressonância magnética ( R M ).