Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.9 - Ex. 57
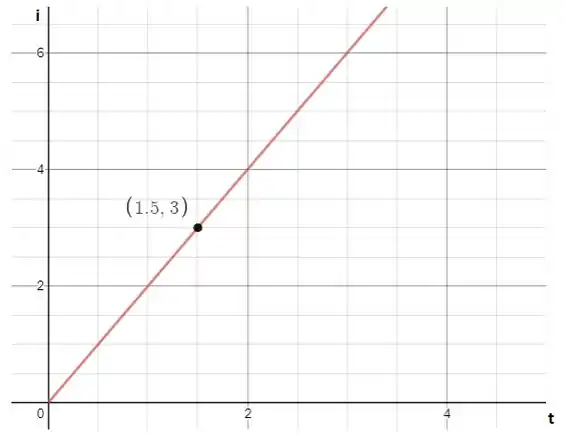
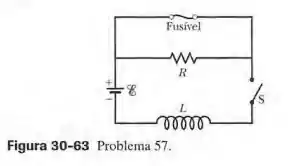
Na Fig. 30-63, , , a força eletromotriz da fonte ideal é e o fusível do ramo superior é um fusível ideal de . A resistência do fusível é zero enquanto a corrente que o atravessa permanece abaixo de . Quando atinge o valor de , o fusível “queima” e passa a apresentar uma resistência infinita. A chave é fechada no instante . (a) Em que instante o fusível queima? (b) Faça um gráfico da corrente no indutor em função do tempo e assinale o instante em que o fusível queima.
Passo 1
Note que este problema não retrata um circuito em série. Assim, não vale a equação
Precisamos achar uma alternativa para resolver o problema.
Como o fusível tem resistência nula antes de queimar, toda a corrente escolher passar por ele e não haverá corrente passando pelo resistor. Assim, pela lei das malhas:
Portanto,
Assim,
Passo 2
No instante em que o fusível queima, :
Portanto,
Passo 3
Fazendo um gráfico da corrente em função do tempo:
