Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.5 - Ex. 53

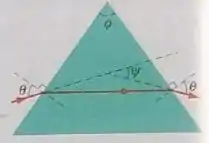
Na fig 33-53 , um raio incide em uma das faces de um prisma triangular de virdro imerso no ar. O ângulo de incidência θ é esclhido de tal forma que o raio emergente faz o mesmo ângulo θ com a normal à outra face. Mostre que o índce de refração n do vidro é dado por

n = s e n 1 2 ψ + ϕ s e n ( 1 2 ϕ ) ,

ϕ é o ângulo do vértice superior do prisma e ψ é o ângulo de desvio, definido como o ângulo entre o raio emergente e o raio incidente. (Nessas condições, o ângulo de desvio ψ tem o menor valor possível, que é denominado ângulo de desvio mínimo.)

Passo 1

Vamos começar?

No ar sabemos que o índice de refração é 1 . Então queremos saber o do vidro. O ângulo de incidência é θ , e vou chamar o ângulo de refração de α . Então pela le de Snell temos:

1 . s e n θ = n s e n α

n = s e n θ s e n α

Passo 2

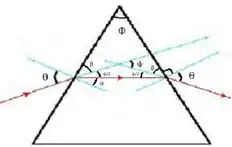Agora vamos ao triâgulo:

Sabemos que a soma de β + ψ 2 + α = 90 ° , então temos que:

β = 90 - α - ψ 2

Por outro lado:

β + ψ 2 + β + ψ 2 + ϕ = 180

Então temos que α é:

90 - α - ψ 2 + ψ 2 + 90 - α - ψ 2 + ψ 2 + ϕ = 180

- 2 α + ϕ = 0

α = ϕ 2

E também do desenho temos que θ = α + ψ 2 , então:

θ = ψ 2 + ϕ 2

Passo 3

Agora juntando os ângulos e substituindo no resultado do índice de refração do passo 1 teremos:

n = s e n θ s e n α = s e n ( ψ 2 + ϕ 2 ) s e n ( ϕ 2 )

Resposta

n = s e n θ s e n α = s e n ( ψ 2 + ϕ 2 ) s e n ( ϕ 2 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig.35-56 mostra uma fibra ótica na qual um núcleo central de plástico, com um índice de refração n 1 = 1,58 , é envolvida por um revestimento de plástico com um índice de refração n 2 = 1,53 . Os r
A Fig.35-57 mostra um jogo de fliperama que foi lançado no Texas. Quando pistolas de lasers são apontadas para o centro de um conjunto de placas de plástico, onde se encontra o alvo, um tatu de barro.
Na Fig. 35-33, um raio luminoso incide com um ângulo θ 1 = 50 ° em uma série de cinco placas transparentes com interfaces paralelas. Para as placas 1 e 3, L 1 = 20 μ m , L 3 = 25 μ m , n 1 = 1,6 e n 3
No modelo simplificado de fibra ótica discutido na Seç. 2.4 (cilindro circular de vidro), calcule o ângulo de incidência θ máximo na face de entrada (fig.) para o qual a luz será guiada dentro da fibr
Quando um raio de sol penetra numa gota de água, ele sofre reflexões múltiplas internas acompanhadas de transmissões parciais para fora. Considere um raio A B C D E que sofre uma única reflexão intern