Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 8

Quando um raio de sol penetra numa gota de água, ele sofre reflexões múltiplas internas acompanhadas de transmissões parciais para fora. Considere um raio A B C D E que sofre uma única reflexão interna antes de emergir da gota (fig.).

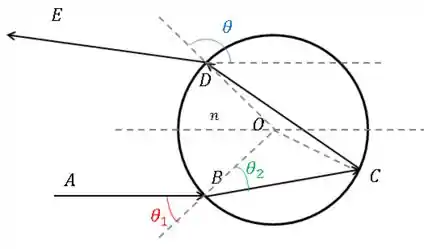
(a) Mostre que o desvio θ do raio emergente D E em relação à direção de incidência A B é dado por

θ = π + 2 θ 1 - 4 θ 2

onde θ 2 é o ângulo de refração associado ao ângulo de incidência θ 1 , (trate a gota como uma esfera de índice de refração n ). O arco-íris primário se forma quando o desvio θ é mínimo.

(b) Mostre que isso acontece para um ângulo de incidência θ 1 R tal que

sen ⁡ θ 1 R = 4 - n 2 3

(c) Calcule o ângulo θ correspondente (ângulo do arco-íris primário) para luz amarela.

Passo 1

a)

primeiro, vamos entender o que é o ângulo de desvio. Bom, pela própria palavra, se um raio tava vindo em uma direção e ai ele sofreu uma reflexão ou refração, que o fez mudar de direção, o ângulo de desvio é o que mede essa mudança.

O ângulo de desvio entre o raio incidente e o emergente da gota é a soma dos desvios do raio em cada etapa da refração e reflexão na gota.

Isto é, o ângulo θ é soma dos desvios que ocorrem em cada ponto da gota.

θ = d B + d C + d D

Vamos ver quanto que vale cada desvio

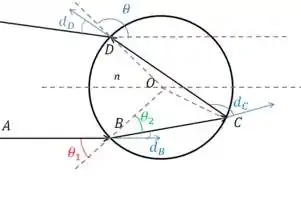
Pra gente descobrir os valores deles, temos que perceber que os triângulos O B C e O D C são isósceles, pois os lados são raios, então os ângulos das bases são iguais:

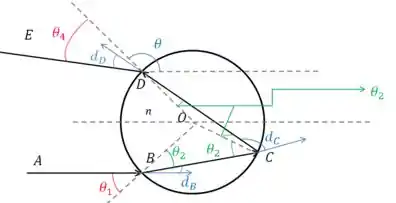
Olhando lá na interface gota-ar no ponto D, marque o ângulo de refração, em relação a normal θ 4 . Ok?

Agora, vamos lá, o ângulo de desvio d B = θ 1 - θ 2 .

Já o d C = 180 ° - 2 θ 2 .

E o d D = θ 4 - θ 2

Ok. Guarda isso aí!

Vamos apliar a lei de snell na interface no ponto B:

n 1 sen ⁡ θ 1 = n sen ⁡ θ 2

Agora, pela lei de snell na interface no ponto D:

n sen ⁡ θ 2 = n 1 sen ⁡ θ 4

Substituindo uma na outra temos que

n 1 sen ⁡ θ 1 = n 1 sen ⁡ θ 4

Então

θ 1 = θ 4

Dessa forma

d D = θ 4 - θ 2

d D = θ 1 - θ 2

Então o desvio total θ vale

θ = d B + d C + d D

θ = θ 1 - θ 2 + 180 ° - 2 θ 2 + θ 1 - θ 2

θ = 2 θ 1 - 4 θ 2 + 180 °

Maravilha!

Passo 2

b)

ele disse pra gente que o arco íris ocorre quando o θ é mínimo. Vamos usar isso, e derivar o θ   em relação a θ 1 e igualar a zero.

d θ d θ 1 = d 2 θ 1 - 4 θ 2 + 180 ° d θ 1

d θ d θ 1 = 2 - 4 d θ 2 d θ 1 = 0

Então

d θ 2 d θ 1 = 1 2

Pela lei de snell no ponto B vimos que

n 1 sen ⁡ θ 1 = n sen ⁡ θ 2

Tomando n 1 = 1 ,

sen ⁡ θ 1 = n sen ⁡ θ 2

θ 2 = a r c s e n sen ⁡ θ 1 n

Vamos derivar em relação a θ 1 e igualar a 1 2 que era o que tinhamos:

d θ 2 d θ 1 = d   a r c s e n sen ⁡ θ 1 n d θ 1 = cos ⁡ θ 1 n 1 - sen ⁡ θ 1 n 2

cos ⁡ θ 1 n 1 - sen ⁡ θ 1 n 2 = 1 2

Elevando ao quadrado:

cos 2 ⁡ θ 1 n 2 1 - sen ⁡ θ 1 n 2 = 1 4

Usando a relação trigonométrica fundamental

1 - sen 2 ⁡ θ 1 1 - sen ⁡ θ 1 n 2 = n 2 4

Arrumando isso:

4 - n 2 = 3 sen 2 ⁡ θ 1

sen ⁡ θ 1 = 4 - n 2 3

Passo 3

c)

como

θ = 2 θ 1 - 4 θ 2 + 180 °

E

θ 2 = a r c s e n sen ⁡ θ 1 n

Temos

θ = 2 θ 1 - 4 a r c s e n sen ⁡ θ 1 n + 180 °

Vimos na letra b que

sen ⁡ θ 1 = 4 - n 2 3

Então

θ 1 = a r c s e n 4 - n 2 3

Então

θ = 2 θ 1 - 4 a r c s e n sen ⁡ θ 1 n + 180 °

θ = 2 a r c s e n 4 - n 2 3 - 4 a r c s e n sen ⁡ a r c s e n 4 - n 2 3 n + 180 °

θ = 2 a r c s e n 4 - n 2 3 - 4 a r c s e n 4 - n 2 3 n + 180 °

Sustituindo n = 1,33 , que é o indice de refração da agua, vemos que

θ = 2 a r c s e n 4 - 1,33 2 3 - 4 a r c s e n 4 - 1,33 2 3 1,33 + 180 °

θ = 137,5 °

Resposta

a)demonstração

b)demonstração

c) θ = 137,5 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 33-51, a luz incide, fazendo um ângulo 81 = 40,1º com a normal, na interface de dois meios transparentes. Parte da luz atravessa as outras três camadas transparentes e parte é refletida para c
Na fig 33-53 , um raio incide em uma das faces de um prisma triangular de virdro imerso no ar. O ângulo de incidência θ é esclhido de tal forma que o raio emergente faz o mesmo ângulo θ com a normal à
Suponha que o ângulo do vértice superior do prisma de vidro da fig 33-53 seja ϕ = 60 ° e que o índice de refração do vidro seja n = 1,6 . (a) Qual é o menor ângulo de incidência θ para o qual um raio
Na figura 33-65, um raio luminoso entra em uma placa de vidro no ponto A, com um ângulo de incidência θ 1 = 45,0 ° , e sofre reflexão interna total no ponto B. De acordo com essas informações, qual é
Na Fig. 33-78, em que n 1=1,70 ,n 2 = 1,50 e n 3 = 1,30 , a luzé refratada do material 1 para o material 2. Se a luz incide no ponto A com o ângulo crítico da interface dos materiais 2 e 3, determine