Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.Problemas Adicionais - Ex. 98
O feixe de um laser, de intensidade , é refletido por uma superfície plana de área , totalmente refletora, cuja normal faz um ângulo com a direção do feixe. Escreva uma expressão para a pressão da radiação do feixe sobre a superfície, , em função da pressão do feixe para .
Passo 1
E aí meus caros(as)! Bora pra mais uma questãozinha dos problemas adicionais do Halliday!
Vamos começar nossa resolução fazendo um esboço do que mais ou menos está acontecendo em nosso problema...
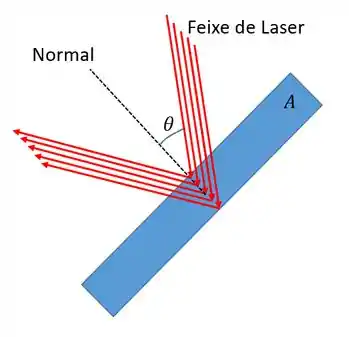
Bom! A questão basicamente nos diz que um feixe de um laser é refletido por uma superfície plana de área , totalmente refletora, cuja normal faz um ângulo com a direção do feixe. E o que a gente tem que fazer é obter uma expressão para a pressão de radiação do feixe.
Pois muito bem! Bora lá!
Tá ligado na área da superfície plana, !? A área da seção reta do feixe, que é paralela à superfície, é dada por .
Se a gente pensar que o feixe incide durante um intervalo de tempo com uma velocidade tal, que chamaremos de , então o volume refletido pela superfície será dado por...
Com isso, podemos achar o momento associado a esse volume, que é dado por...
Passo 2
E como o nosso feixe de laser está sendo refletido, então a variação de momento total do sistema é dada por...
Sendo assim...
Passo 3
Por fim, para achar a pressão de radiação , basta dividir a força resultande de absorção pela área da superfície refletora. Logo;
Só que a relação acima também pode ser escrita como...
Desse modo, substituindo o do ...
Conseguimos obter uma fórmula madura para a pressão de radiação. Agora, coloca pra ver o que acontece!?
Nós obtemos que para , a pressão de radiação vale . E esse valor é justamente aquele mencionado no enunciado. E então, ficamos com a seguinte expressão final...
Até a próxima guys!