Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.Problemas adicionais - Ex. 109
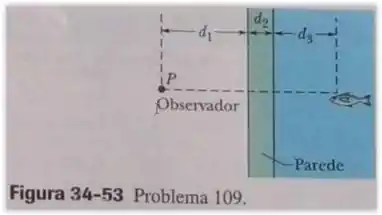
Na Fig. 34-53, um observador, situado no ponto , olha para um peixe através da parede de vidro de um aquário. O observador está na mesma horizontal que o peixe; o índice de refração do vidro é e o da água é . As distâncias são , e . (a) Do ponto de vista do peixe, a que distância parece estar um observador? (Sugestão: o observador é o objeto. A luz proveniente do objeto passa pela superfície externa da parede do aquário, que se comporta como uma superfície refratora. Determine a imagem produzida por essa superfície. Em Seguida, trate essa imagem como um objeto cuja luz passa pela superfície refratora. Determine a distância da imagem produzida por essa superfície, que é a resposta pedida.) (b) Do ponto de vista do observador, a que distância parece estar o peixe?
Passo 1
Olá amiguinho,
Quando estamos lidando com superfícies refratoras esféricas, temos como referência a Eq.34-8
Onde é a distância do objeto até a superfície, é a distância entre a imagem e a superfície e o raio da superfície.
Passo 2
- Seguindo a sugestão do autor vamos calcular onde a primeira imagem, depois de passar pela superfície externa, se forma. Como são superfície planas, dizemos que e lembrando que o índice d refração do ar é 1
- Agora temos que seguir a sugestão, porém seguindo o passo a passo reverso.
Assim temos que
Indicando que a imagem se forma a esquerda da nossa superfície. Logo nosso novo “objeto” que é visto pela superfície interna está a uma distância
Tomando novamente a relação do passo 1, temos
O que nos leva a
Como o peixe está a 6,8 cm da superfície, ele vê o observado a uma distância
Passo 3
Vamos calcular onde a primeira imagem do peixe se forma ao passar pela superfície interior do aquário.
Onde a distância que a superfície externa “vê” o novo peixe será . Assim temos que agora teremos
Assim o observador verá o peixe a uma distância de
Ou seja, o observador vê o peixe mais perto do que o peixe vê o observador