Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.3 - Ex. 27
Um carregador de supermercado empurra uma caixa com massa de sobre uma superfície horizontal com uma velocidade constante de . O coeficiente de atrito cinético entre a caixa e a superfície é . a) Que força horizontal o trabalhador deve aplicar para manter o movimento? b) Se a força calculada na parte a) for removida, que distância a caixa deslizará até parar?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar a (a) for��a horizontal que o trabalhador deve aplicar para manter o movimento e (b) a distância que a caixa deslizará até parar, considerando que a a força calculada na parte a) seja removida.
Sabemos que velocidade constante implica na aceleração . A força de atrito é direcionada para o lado oposto ao movimento da caixa. Como a caixa está deslizando , temos que o atrito é cinético, . Então, vamos considerar sendo a força horizontal aplicada pelo trabalhador e temos o seguinte diagrama de corpo livre:
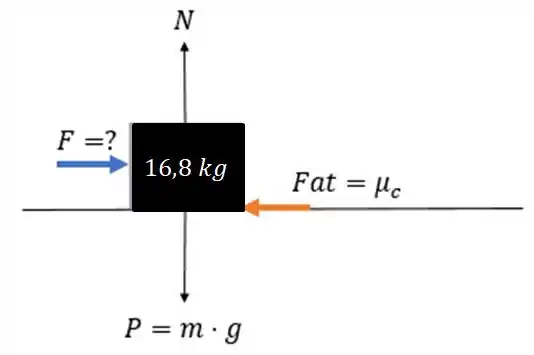
Assim, vamos usar a segunda lei de Newton, para analisar as forças atuantes no eixo e no eixo e encontrar o valor da força . Depois, vamos considerar que ela seja nula e calcular a distância pedida.
Vamos lá!
Passo 2
a) Vamos aplicar a 2º Lei de Newton na caixa:
Para o eixo :
Mas a força peso é dada por . Assim, temos:
Como a velocidade é constante, essa aceleração é nula e ficamos com:
Logo,
Então, a força de atrito será dada por:
Passo 3
Para o eixo , vamos ter:
Considerando a aceleração nula:
E substutindo a força de atrito encontrada acima, temos:
Portanto, temos que a força, , aplicada pelo trabalhador deverá ser:
E substituindo os dados, encontramos:
Passo 4
b) Bom, agora vamos remover a Força, . Então, Agora a única força horizontal na caixa é a força de atrito cinético .
Precisamos aplicar a 2º Lei de Newton na caixa, para que possamos calcular a sua aceleração, .
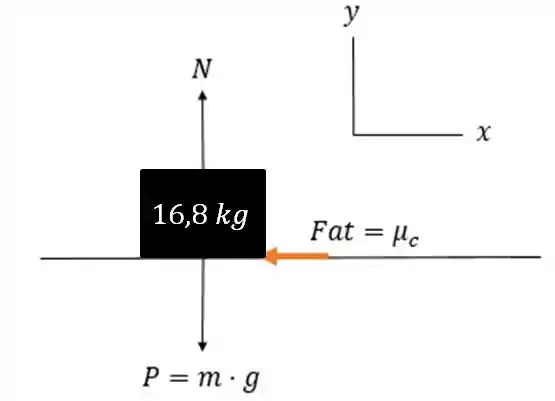
Quando tivermos a aceleração, podemos encontrar a distância usando a equação de Torricelli.
Sabemos que a força de atrito é:
Então, vamos calcular a aceleração. Para isso, vamos utilizar a segunda lei de Newton no eixo :
Se dividirmos tudo por , ficamos com:
E substituindo os valores, temos:
Passo 5
Como encontramos a aceleração, podemos calular a distancia percorrida pela caixa até que ela pare. Como não temos o tempo, , podemos calcular através da equação de Torricelli:
Onde é a velocidade final na direção horizontal, é a velocidade inicial e é a aceleração encontrada no passo anterior. Assim, isolando a distância , temos:
Portanto, com os valores dados, temos:
Valeu, galera! Até a próxima! 😉