Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.3 - Ex. 31

Um carregador de supermercado empurra uma caixa com massa de 11,2   k g sobre uma superfície horizontal com uma velocidade constante de 3,50   m / s . O coeficiente de atrito cinético entre a caixa e a superfície é 0,20 . a) Que força horizontal o trabalhador deve aplicar para manter o movimento? b) Se a força calculada na parte a) for removida, que distância a caixa deslizará até parar?

Passo 1

Fala aí! tudo certinho?

Nesse problema temos um carregador de supermercado que empurra uma caixa com massa de 11,2   k g sobre uma superfície horizontal com uma velocidade constante de 3,50   m / s . O coeficiente de atrito cinético entre a caixa e a superfície é 0,20 .

A partir daí queremos saber que força horizontal o trabalhador deve aplicar para manter o movimento e também se a força calculada for removida, que distância a caixa deslizará até parar.

Parece complicado?

Sabemos que velocidade constante implica a = 0 .

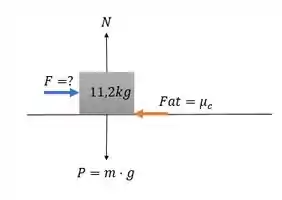
A força de atrito é direcionada oposto ao movimento da caixa.

Como a caixa está deslizando , temos que o atrito é cinético. μ c . E sabemos que o atrito cinético

Vamos fazer F sendo a força horizontal aplicada pelo trabalhador.

Bora lá!

Passo 2

  1. Vamos aplicar as 2º Lei de Newton sob a caixa:

  • Para o eixo y :

    • F y = m ⋅ a y

    ⇒     N - P = m ⋅ a

    ⇒ N - m ⋅ g = m ⋅ a  

    ⇒ N - m ⋅ g = 0

    ⇒     N = m ⋅ g    

    Então,

    F a t = μ c ⋅ N = μ c ⋅ m ⋅ g

  • Para o eixo x :

F x = m ⋅ a x

F - F a t = m ⋅ 0

⇒ F = F a t

Portanto, temos que a força, F , aplicada pelo trabalhador deverá ser:

F = F a t = μ c ⋅ m ⋅ g = 0,20 ⋅ 11,2 k g ⋅ 9,8 m / s 2 )

F = 22 N

Tranquilo até aqui?

Passo 3

  • Bom, agora vamos remover a Força, F . Então, Agora a única força horizontal na caixa é a força de atrito cinético μ c .

    • Precisamos aplicar a 2º Lei de Newton na caixa, para que possamos calcular a sua aceleração, a .

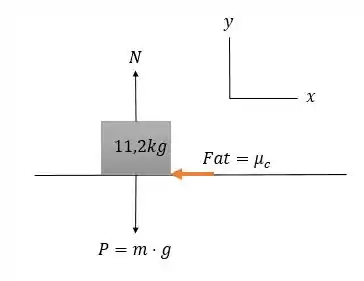
    Quando tivermos a aceleração, podemos encontrar a distância usando uma constante

    equação de aceleração.

    Sabemos que a força de atrito é:

    F a t = μ c ⋅ m ⋅ g

    Então, vamos calcular a aceleração. Para isso, vamos utilizar a primeira lei de Newton no eixo x :

    F x = m ⋅ a x

    ⇒   - F a t = m ⋅ a x

    ⇒   - μ c ⋅ m ⋅ g = m ⋅ a x

    Se dividirmos tudo por m :

    - μ c ⋅ g = a x

    a x = - 0,20 ⋅ ( 9,8 m / s 2 )

    a x = - 1,96 m / s 2

    Show?

    Passo 4

    Como encontramos a aceleração, podemos calular a distancia percorrida pela caixa até que ela pare. Como não temos o tempo, t , podemos calcular através da equação de Torricelli:

    v x 2 = v 0 x 2 + 2 ⋅ a x ⋅ ∆ S

    ⇒   ∆ S = v x 2 - v 0 x 2 2 ⋅ a x

    Portanto,

    ∆ S = 0 - 3,50 m s 2 2 ⋅ - 1,96 m s 2

    ∆ S = 3,1 m

    E aí! entendeu tudo? Responde Aí!

    Resposta

    F = 22 N

    ∆ S = 3,1 m

    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    Um bloco de massa m=2,00k g repousa na extremidade esquerda de outro de massa M=8,00k g . O coeficiente do atrito cinético entre os dois blocos é 0,300 e a superfície em que o bloco de 8,00k g repousa
    2 . Em um modelo de laboratório de carros deslizando até parar, dados são obtidos em quatro experimentos usando dois blocos. Eles têm massas idênticas, mas diferentes coeficientes de atrito cinético c
    Quando os três blocos da Fig. 6-29 são liberados a partir do repouso, aceleram com um módulo de 0,500m / s 2 . O bloco 1 tem massa M , o bloco 2 tem massa 2 M e o bloco 3 tem massa 2 M . Qual é o coef
    5.14E Suponha que entre o bloco e a superfície da rampa da Figura 5.14 haja um coeficiente de atrito cinético μ ctg ⁡ ϕ . Sendo v 0 a velocidade inicial do bloco, calcule: A) o tempo gasto no deslizam
    Uma caixa com massa de 10,0 kg se move em uma rampa inclinada em um ângulo de 55,0º acima da horizontal. O coeficiente de atrito cinético entre a caixa e a superfície da rampa é μc 0,300. Calcule o mó