Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.5 - Ex. 27

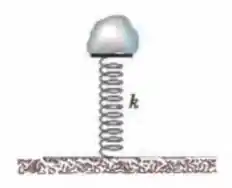
A Fig. 8-34 mostra uma pedra de 8,00   k g em repouso sobre uma mola. A mola é comprimida 10,0   c m pela pedra. (a) Qual é a constante elástica da mola? (b) A pedra é empurrada mais 30   c m para baixo e liberada. Qual é a energia potencial elástica da mola comprimida antes de ser liberada? (c) Qual é a variação da energia potencial gravitacional do sistema pedra-Terra quando a pedra se desloca do ponto onde foi liberada até a altura máxima? (d) Qual é essa altura máxima, medida a partir do ponto onde a pedra foi liberada?

Passo 1

Como a pedra está em repouso sobre a mola, então há ali um equilíbrio de forças. Portanto, aplicando a segunda lei de Newton, temos:

e i x o   v e r t i c a l :       F e l - P = 0

k x = m g

Isolando k :

k = m g x

Substituindo os valores dados na questão:

k = 8 × 9,8 0,1 = 784   N / m

Passo 2

A equação da energia potencial elástica é:

U e l = k x 2 2

Sabendo a constante elástica da mola e também o deslocamento da mola em função da sua posição natural, então a energia potencial no momento de compressão máxima é:

U e l m á x = 784 × 0,3 + 0,1 2 2 = 62,7   J

Passo 3

Devemos perceber que no momento em que a pedra é liberada e no momento que a atinge a altura máxima a velocidade é nula. Sabendo que durante estes instantes só atuam sobre a pedra a força elástica e a força peso, que são conservativas, então podemos aplicar a conservação da energia mecânica:

E M 0 = E M f

k x m á x 2 2 = m g h m á x

62,7 = 8 × 9,8 × h m á x

Isolando h m á x :

h m á x = 62,7 8 × 9,8 = 0,8   m

Passo 4

Com a altura máxima calculada, podemos determinar a variação da energia potencial entre os instantes de compressão máxima e de altura máxima, considerando o ponto de compressão máxima como y = 0 :

∆ U g = m g h m á x - m g h 0 = m g h m á x - 0

∆ U g = 8 × 9,8 × 0,8 = 62,7   J

Resposta

  1. k = 784   N / m ;
  2. U e l m á x = 62,7   J ;
  3. ∆ U g = 62,7   J ;
  4. h m á x = 0,8   m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pula-pula de uma criança (Fig. P7.69) armazena energia em uma mola com uma constante elástica de 2,50 ×10 4N / m . Na posição A( x=– 0,100m ), a compressão da mola é máxima, e a criança está momenta
Começando do repouso, uma pessoa de 64,0k g pula de bungee jump de um balão de ar amarrado 65,0m acima do solo. A corda do bungee tem massa desprezível e comprimento esticado de 25,8m . Uma ponta é am
Um bloco de massa M está em repouso sobre uma mesa. Ele é preso na ponta de baixo de uma mola leve e vertical. A ponta de cima da mola está presa a um bloco de massa m . O bloco de cima é empurrado pa
A constante elástica da mola de uma espingarda de mola é k = 1,0 N/cm. Qual deve ser o comprimento de compressão da mola para que ela seja capaz de atirar projéteis de massa igual a 0,50 g com velocid
Calcule a variação da energia potencial de uma pessoa de 70 kg ao subir uma montanha de 1,0 km de altura. Compare o resultado com a energia ( E = 1,3x10 6J ) absorvida pelo organismo ao digerir um ham