Começando do repouso, uma pessoa de pula de bungee jump de um balão de ar amarrado acima do solo. A corda do bungee tem massa desprezível e comprimento esticado de . Uma ponta é amarrada à cesta do balão e a outra, a um engate ao redor do corpo da pessoa. A corda é modelada como uma mola que obedece à lei de Hooke, com uma constante de mola de , e o corpo da pessoa é modelado como uma partícula. O balão de ar quente não se move. (a) Expresse a energia potencial gravitacional do sistema pessoa-Terra como uma função da altura variável da pessoa acima do solo. (b) Expresse a energia potencial elástica da corda como uma função de . (c) Expresse a energia potencial total do sistema pessoa-corda-Terra como uma função de . (d) Faça um gráfico da energia potencial gravitacional, elástica e total como funções de . (e) Suponha que a resistência do ar seja desprezível. Determine a altura mínima da pessoa acima do solo durante seu mergulho. (f) O gráfico de energia potencial mostra alguma posição, ou posições, de equilíbrio? Caso mostre, em que posições verticais? Elas são estáveis ou instáveis? (g) Determine a velocidade máxima da pessoa que está saltando.

Letra b:

Na altura original e em todas as alturas acima de , o cabo não está esticado e . Abaixo de 39,2m, a extensão do cabo é dada por , então a energia elástica é:

Letra c:

Para :

Para :

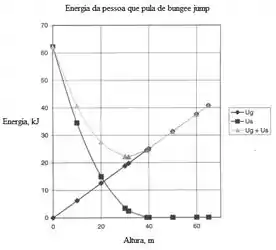
Letra d:

Veja o gráfico:

Letra e:

Na altura mínima, o saltador tem energia cinética zero e o sistema tem a mesma energia total que tinha quando o saltador estava em seu ponto de partida. torna-se:

Letra f:

A energia potencial total tem um mínimo, representando uma posição de equilíbrio estável. Para encontrá-lo, precisamos de Suprimindo unidades, temos:

Letra g:

A energia cinética máxima ocorre na energia potencial mínima. Entre o ponto de salto e este local, temos: