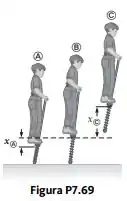
O pula-pula de uma criança (Fig. P7.69) armazena energia em uma mola com uma constante elástica de . Na posição A(), a compressão da mola é máxima, e a criança está momentaneamente em repouso. Na posição B(), a mola é relaxada, e a criança se move para cima. Na posição C, a criança está de novo momentaneamente em repouso no topo do salto. A massa combinada da criança e do pula-pula é . Embora ela tenha de se debruçar para a frente para permanecer equilibrado, o ângulo é pequeno, então vamos supor que o pula-pula seja vertical. Também suponha que o menino não dobre as pernas durante o movimento. (a) Calcule a energia total do sistema criança-pula-pula-Terra, considerando as energias gravitacional e potencial elástica como zero para . (b) Determine . (c) Calcule a velocidade da criança em . (d) Determine o valor de para o qual a energia cinética do sistema seja máxima. (e) Calcule a velocidade máxima para cima da criança.

Letra b:

Uma vez que apenas forças conservativas estão envolvidas, a energia total do sistema criança-pula-pula-terra no ponto C é o mesmo que no ponto A:

Letra c:

Letra d:

A energia do sistema para configurações em que a mola é comprimida é:

onde x é a distância de compressão da mola. Para encontrar a posição x para a qual a energia cinética é máxima, resolva esta expressão para K, diferencie em relação a x, e defina o resultado igual a zero:

Como este é o valor para a distância de compressão da mola, esta posição é 0.98 cm abaixo de x = 0.

em

Letra e: