Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.8 - Ex. 62
Na Fig. 8-55, um bloco é liberado a partir do repouso a uma altura , desce uma rampa sem atrito e chega a um primeiro trecho plano, de comprimento , onde o coeficiente de atrito cinético é . Se o bloco ainda está se movendo, desce uma segunda rampa sem atrito, de altura , e chega a um segundo trecho plano, onde o coeficiente de atrito cinético também é . Se o bloco ainda está se movendo, sobe uma rampa sem atrito até parar (momentaneamente). Onde o bloco para? Se a parada final é em um trecho plano, diga em qual deles e calcule a distância que o bloco percorre a partir da extremidade esquerda desse platô. Se o bloco alcança a rampa, calcule a altura acima do trecho plano mais baixo onde o bloco para momentaneamente.
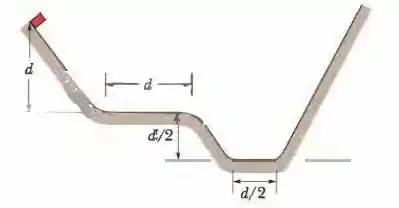
Figura 8-55 Problema 64.
Passo 1
Oi, galerinha! Tudo bom? Nessa questão vamos usar a conservação da energia e analisar cada treixo do caminho.
Na rampa, temos apenas a conversão da energia potencial gravitacional em energia cinética, logo
Passo 2
Do começo ao final do plano, temos perda de energia cinética devido ao atrito
Como vimos na equação 1 que a energia cinética será igual a potencial, temos,
Como,
E como
Passo 3
Na rampa, temos novamente a transformação de energia potencial gravitacional em energia cinética, então
Passo 4
Ao final do plano, parte da energia cinética é dissipada pelo atrito. Dessa forma, no início da rampa, a energia cinética será
Como
Passo 5
Estamos interessados em saber onde o bloco para na rampa. Nesse instante, toda a energia cinética será transformada em energia potencial gravitacional, logo
Para
Resposta
O bloco alcança a rampa e para quando .