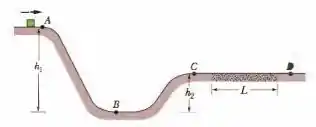
Na Fig. 8-65, um pequeno bloco parte do ponto com uma velocidade de . O percurso é sem atrito até chegar o trecho de comprimento , onde o coeficiente de atrito cinético é . As alturas indicadas são e . Qual é a velocidade do bloco (a) no ponto e (b) no ponto? (c) O bloco atinge o ponto ? Caso a resposta seja afirmativa, determine a velocidade do bloco nesse ponto; caso a resposta seja negativa, calcule a distância que o bloco percorre na parte com atrito.

Utilizando um raciocínio análogo ao do item anterior , sabemos a velocidade no ponto pode ser calculada através da relação :

Bom pessoal, reparem que a partir do ponto a pista é horizontal, a energia cinética do bloco no início do trecho “acidentado” é a mesma que o bloco possuía no ponto , que podemos calcular usando o resultado do item (b):

Note que a massa na equação será cancelada , uma vez que sabemos que e supondo que toda a energia cinética é transformada em energia térmica, temos:

para . Fazendo , obtemos , que é realmente menor que (dado no problema como sendo ). Concluímos que o bloco não chega ao ponto e a distância que percorre no trecho com atrito é.