Uma pedra que pesa é lançada verticalmente a partir do nível do solo com uma velocidade inicial de e o arrasto do ar sobre ela é de durante todo o percurso. Determine (a) a altura máxima alcançada pela pedra e (b) sua velocidade imediatamente antes de se chocar com o solo.

Começando pela letra a), vamos encontrar a altura máxima desse movimento:

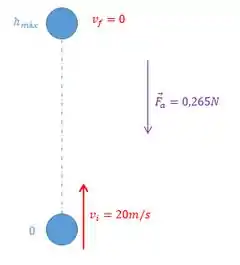
Considerando o nível de referência como o solo, não teremos energia potencial gravitacional inicial, pois sua altura inicial é zero. Na altura máxima, a velocidade é zero e por isso a energia cinética final é zero. Sendo assim, teremos:

Agora, com relação ao trabalho da força não conservativa, ele vai ser dado como:

Como a força de arraste aponta para baixo e o deslocamento aponta para cima, teremos:

Esse trabalho tem um valor negativo, o que faz sentido, afinal a força de arraste diminui a energia mecânica do sistema.

Agora voltando para a nossa equação da energia:

A massa não foi dada, mas foi dado o valor do peso, portanto:

Agora é só substituir e correr pro abraço:

Portanto, a altura máxima foi de

Para a letra b), queremos encontrar a velocidade no momento que a bola chega ao solo novamente.

Podemos fazer isso, a partir do momento que a bola está na altura máxima até o momento que ela chega ao solo.

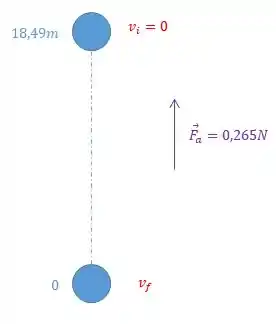
Usando a equação da energia, teremos:

Não haverá cinética inicial e não haverá potencial final, portanto:

Aonde o trabalho da força de arraste, será dado como:

E novamente, a força de arraste é contrária ao deslocamento, portanto:

Substituindo na expressão, teremos:

Portanto a velocidade com que a bola chega ao solo de volta é de . Um pouco menor do que a velocidade com que ela saiu, que era de e isso acontece pois a força de arraste fez com que se perdesse energia mecânica ao longo do movimento (se não houvesse arraste, era para a bola ter retornado com a mesma velocidade).