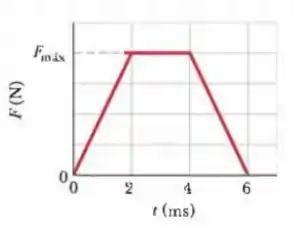
A Fig. 9-53 mostra um gráfico aproximado do módulo da força F em função do tempo t para uma colisão de uma Superbola de 58g com uma parede. A velocidade inicial da bola é 34m / s , perpendicular à parede; ela ricocheteia praticamente com a mesma velocidade escalar, também perpendicular à parede. Quanto vale F m á x á , o módulo máximo da força exercida pela parede sobre a bola durante a colisão?

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.6 - Ex. 37

A Fig. 9-53 mostra um gráfico aproximado do módulo da força em função do tempo para uma colisão de uma Superbola de com uma parede. A velocidade inicial da bola é , perpendicular à parede; ela ricocheteia praticamente com a mesma velocidade escalar, também perpendicular à parede. Quanto vale , o módulo máximo da força exercida pela parede sobre a bola durante a colisão?

Passo 1

Oi, galerinha! Tudo bom? Primeiro, vamos tomar como referência o sentido positivo do nosso eixo de referência como sendo o sentido de movimento da bola após ricochetear.

O gráfico mostra que a força varia com o tempo. Deste modo, podemos determinar o impulso de uma força variável através da integral:

E lembrando também que a integral, por definição, é igual a área da função. Neste caso, nós conhecemos essa figura geométrica, então podemos achar o impulso separando a área do trapézio em dois triângulos e um retângulo:

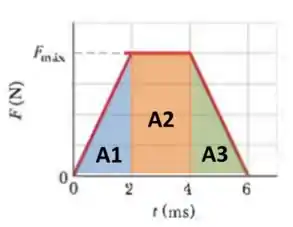
Com isso temos:

Passo 2

Aplicando agora o teorema do impulso momento linear, sabendo que a velocidade inicial é e a velocidade final é :

Como, e , então isolando :

Assim:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma máquina de Atwood, cuja polia é sem massa e sem atrito e cujo cordão é sem massa, tem um corpo de 2,00k g suspenso de um lado e um corpo de 4,00 kg suspenso do outro lado. (a) Qual é a rapidez de

Uma mulher de 60 k g está na parte de trás de uma balsa de 120 k g e de 6,0 m de comprimento, que flutua em águas calmas. A balsa está a 0,50 m de um cais fixo, como mostrado na figura 8-52. (a) A mul

A figura mostra um canhão da Primeira Guerra Mundial montado sobre um vagonete e preparado para atirar uma bala a um ângulo de 30 ° acima da horizontal. Com o vagão inicialmente em repouso sobre um tr

Uma senquencia de contas eláticas de vidro, cada uma de massa 0,50g , sai de um tubo horizontal a uma taxa de 100 por segundo (veja a Figura 8-57). As contas caem de uma altura de 0,50m sobre um prato

Um haltere, constituído de duas bolas de massa m ligadas por uma barra sem massa de 1,00m de comprimento, é colocado sobre um piso sem atrito e apoiado sobre uma parede sem atrito, com uma das bolas d