Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 102

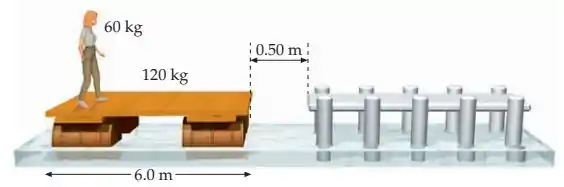
Uma mulher de 60 k g está na parte de trás de uma balsa de 120 k g e de 6,0 m de comprimento, que flutua em águas calmas. A balsa está a 0,50 m de um cais fixo, como mostrado na figura 8-52. (a) A mulher caminha para a frente da balsa e para. Qual é a distância, agora, da balsa ao cais? (b) Enquanto a mulher caminha, ela mantém uma rapidez constante de 3,0 m / s em relação à balsa. Determine a energia cinética total do sistema (mulher mais balsa) e compare sua resposta com o valor que teria a energia cinética se a mulher caminhasse a 3,0 m / s sobre a balsa presa ao cais. (c) De onde vêm essas energias cinéticas e para onde vão quando a mulher para na frente da balsa? (d) Quando em terra, a mulher é capaz de lançar um peso de chumbo até uma distância de 6,0 m . Agora, na parte de trás da balsa, ela atira o peso para a frente com a mesma velocidade em relação a ela que ele tinha quando foi lançado em terra. Aproximadamente, em que ponto o peso irá cair?

Passo 1

  1. Vamos lá, essa é bem cascuda. Vamos chamar de m a massa da mulher e M a massa da balsa. A distância da balsa ao píer depois de a mulher andar para a frente da balsa:

    2. d = 0,50 + x m , f

    A posição do centro de massa vai ser dada por:

    x c m = m x m , i + M x b , i m + M

    Como não há força externa, o centro de massa não se move.

    m x m , i + M x b , i = m x m , f + M x b , f

    Isolando x m , f :

    x m , f = m x m , i m + M

    Substituindo valores:

    x m , f = 60 × 6 60 + 120 = 2.0 m

    Na primeira equação:

    d = 0.50 + 2.0

    d = 2.5 m

    Passo 2

  2. A energia cinética da situação é:

    3. K = m v 2 2 + M V 2 2

    Agora a gente acha essas velocidades. Se liga: as duas vão ser em relação ao cais.

    v = x m , f - x m , i t = 2.0 - 6.0 2

    v = - 2.0 m / s

    V = x b , f - x b , i t = 2.50 - 0.50 2

    V = 1.0 m / s

    Substituindo:

    K = 60 - 2.0 2 2 + 120 × 1.0 2 2 = 0.18 k J

    Com a balsa amarrada ao píer:

    K = m v 2 2 = 60 × 3.0 2 2 = 0.27 k J

    Passo 3

  3. Toda a energia provém da energia que a mulher transmite ao sistema.

    4. Passo 4

  4. Depois que o tiro do peso de chumbo deixa a mão da mulher, o sistema constitui uma referencial inercial. Nesse referencial, o tiro tem a mesma velocidade inicial que tinha o tiro de 6.0 m no referencial da terra. Assim, no referencial do sistema mulher-balsa, o tiro também tem um alcance de 6,0 m , e cai em frente à balsa.

Resposta

  1. d = 2.5 m
  2. K t o t a l = 0.18 k J e K b a l s a - p a r a d a = 0.27 k J
  3. Toda a energia provém da energia que a mulher transmite ao sistema.
  4. 6.0 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola de 1,2k g cai verticalmente em um piso com uma velocidade de 25m / s e ricocheteia com uma velocidade inicial de 10m / s . (a) Qual é o impulso recebido pela bola durante o contato com o piso
No tae-kwon-do, a mão de um atleta atinge o alvo com uma velocidade de 13m / s e para após 5,0m s . Suponha que, durante o choque, a mão é independente do braço e tem uma massa de 0,70k g . Determine
Em uma brincadeira comum, mas muito perigosa, alguém puxa uma cadeira quando uma pessoa está prestes a se sentar, fazendo com que a vitima se estatele no chão. Suponha que a vitima tem 70k g , cai de
Uma força no sentido negativo de um eixo x é aplicada por 27m s a uma bola de 0,40k g que estava se movendo a 14m / s no sentido positivo do eixo. O módulo da força é variável e o impulso tem um módul
Em fevereiro de 1955, um paraquedista saltou de um avião, caiu 370m sem conseguir abrir o paraquedas e aterrissou em um campo de neve, sofrendo apenas pequenas escoriações. Suponha que a velocidade do