Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.Problemas Adicionais - Ex. 131

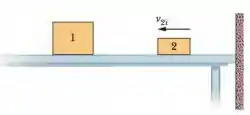
Na Fig. 9-80, o bloco 1, de massa m 1   =   6,6   k g , está em repouso sobre uma mesa sem atrito que está encostada em uma parede. O bloco 2, de massa m 2 , está posicionado entre o bloco 1 e a parede e desliza para a esquerda em direção ao bloco 1 com velocidade constante v 2 i , Determine o valor de m 2 para o qual os dois blocos se movem com a mesma velocidade após o bloco 2 colidir uma vez com o bloco 1 e uma vez com a parede. Suponha que as colisões são elásticas (a colisão com a parede não muda a velocidade escalar do bloco 2).

Passo 1

Primeiro de tudo vamos escrever a equação de conservação de energia cinética já que as colisões são elásticas

m 1 v 1 i 2 2 + m 2 v 2 i 2 2 = m 1 v 1 f 2 2 + m 2 v 2 f 2 2

Sabemos que v 1 i = 0 , então:

m 2 v 2 i 2 = m 1 v 1 f 2 + m 2 v 2 f 2

Agora usando a conservação de momento linear

m 2 v 2 i = m 1 v 1 f + m 2 v 2 f

(Lembrando que v 1 i = 0 )

Passo 2

Na equação do momento vamos isolar v 1 f

v 1 f = m 2 m 1 v 2 i - v 2 f

E vamos jogar na equação que veio da conservação de energia

m 2 v 2 i 2 = m 1 v 1 f 2 + m 2 v 2 f 2

m 2 v 2 i 2 = m 1 m 2 m 1 v 2 i - v 2 f 2 + m 2 v 2 f 2

m 2 v 2 i 2 - m 2 v 2 f 2 = m 1 m 2 m 1 v 2 i - v 2 f 2

m 2 v 2 i 2 - v 2 f 2 = m 2 2 m 1 v 2 i - v 2 f 2 → v 2 i 2 - v 2 f 2 = m 2 m 1 v 2 i - v 2 f 2

Agora vamos fazer uma diferença de quadrados no lado esquerdo escrevendo

v 2 i 2 - v 2 f 2 = v 2 i - v 2 f v 2 i + v 2 f

Isso facilita a nossa vida por que do lado direito temos a diferença ao quadrado!

v 2 i - v 2 f v 2 i + v 2 f = m 2 m 1 v 2 i - v 2 f 2 → v 2 i + v 2 f = m 2 m 1 v 2 i - v 2 f

Agora sim, dá pra isolar v 2 f ! Multiplicando cruzado essa expressão

m 1 v 2 i + m 1 v 2 f = m 2 v 2 i - m 2 v 2 f

m 1 + m 2 v 2 f = m 2 - m 1 v 2 i

v 2 f = m 2 - m 1 v 2 i m 1 + m 2

Voltando para v 1 f

v 1 f = m 2 m 1 v 2 i - v 2 f = m 2 m 1 v 2 i - m 2 - m 1 v 2 i m 1 + m 2

v 1 f = m 2 m 1 m 1 + m 2 - m 2 - m 1 m 1 + m 2   v 2 i

v 1 f = m 2 m 1 2 m 1 m 1 + m 2   v 2 i = 2 m 2 m 1 + m 2   v 2 i

Em resumo:

v 1 f = 2 m 2 m 1 + m 2 v 2 i             v 2 f = m 2 - m 1 m 1 + m 2 v 2 i

Passo 3

Bom pessoal , sabemos que a velocidade do bloco 2 depois de colidir com parede é – v 2 f . De acordo com o enunciado, devemos ter v 1 f = - v 2 f , ou seja :

2 m 2 m 1 + m 2 v 2 i = - m 2 - m 1 m 1 + m 2 v 2 i

o que nos dá :

2 m 2 = - m 2 - m 1

m 2 = m 1 3

Para m 1   =   6,6   k g , obtemos que m 2   =   2,2   k g .

Resposta

m 2   =   2,2   k g

Tranquilo galera? Bora resolver mais questões então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola de borracha com massa m é liberada do repouso a uma altura h acima do solo. Após o primeiro quique, ela sobe a 90 % da sua altura original. Qual impulso (módulo, direção e sentido) o solo exe
Uma bola de massa M que se move horizontalmente a 5,0m / s colide elasticamente com um bloco de massa 3 M , que está inicialmente suspenso em repouso do teto por um fio de 50,0c m . Ache o ângulo máxi
As esferas A (massa 0,020k g ), B (massa 0,030k g ) e C (massa 0,050k g ) se aproximam da origem deslizando sobre uma mesa de ar sem atrito (Figura 8.41 ). As velocidades iniciais de A e de B são indi
Um nêutron de massa m colide frontalmente com um núcleo de massa M , que está inicialmente em repouso. a) Mostre que, se a energia cinética inicial do nêutron fosse K 0 , a energia cinéticaque ele per
Um carrinho de estrada de ferro, impulsionado manualmente, move-se ao longo de um trilho horizontal sem atrito e com resistência do ar desprezível. Nos casos a seguir, o carrinho possuimassa total (ca