Um carrinho de estrada de ferro, impulsionado manualmente, move-se ao longo de um trilho horizontal sem atrito e com resistência do ar desprezível. Nos casos a seguir, o carrinho possui
massa total (carro mais tudo que está em seu interior) igual a 200 kg e se desloca a 5,0 m/s de oeste para leste. Calcule a velocidade final do carrinho em cada caso, supondo que ele não abandone os trilhos. a) Um corpo com 25,0 kg de massa é lançado lateralmente para fora do carrinho com velocidade de módulo igual a 2,0 m/s em relação à velocidade inicial do carrinho.
b) Um corpo com 25,0 kg de massa é lançado para fora do carrinho em sentido contrário ao do seu movimento e com velocidade de módulo igual a 5,0 m/s em relação à velocidade inicial ao carrinho. c) Um corpo com 25,0 kg de massa é lançado para dentro do carrinho com velocidade de módulo igual a 6,0 m/s em relação ao solo e com sentido contrário ao da velocidade inicial
do carrinho.
Passo 1
Vamos usar um sistema de coordenadas conectado ao chão. Tomemos o para o leste (ao longo das trilhas) e o a norte (paralelo ao solo e perpendicular às faixas). Então é conservado e não é conservada, devido à força lateral exercida pelos trilhos, a força que mantém o carro de mão nos trilhos.
Passo 2
- Seja A a massa de e B o carro (massa ). Depois que a massa é jogada de lado em relação para o carro, ele ainda tem o mesmo componente leste de velocidade , como tinha antes de ser lançado.
- Como estamos aplicando nas coordenadas ligadas ao solo, precisamos da velocidade final de Um parente no chão. Usando a equação de adição de velocidade relativa. Em seguida, usando para encontrar velocidade final do carro.
- Seja A a massa de e B o carro
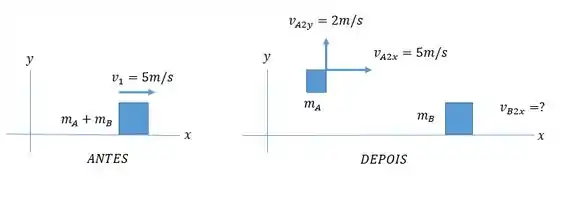
Como é conservado, então:
Então,
Isso implica que:
A velocidade final do carro é de , leste (inalterada).
Passo 3
Então,
Com e (menos uma vez que a massa está se movendo para oeste em relação ao carro). Isso nos dá que:
a massa está em repouso em relação à terra depois que ela é lançada para trás do carro.
No item a):
Agora,
Então,
Isso implica que:
A velocidade final do carro é , a leste.
O lançador exerce uma força na direção , de modo que a massa exerce uma força sobre ele na direção e ele e o carro aceleram.
Passo 4
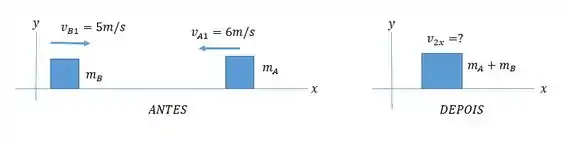
Como é conservado, então,
Isso implica que:
E
A velocidade final do carro é de , a leste.
Como a massa tem negativo, reduz o total de do sistema e o carro diminui a velocidade.
Resposta
- A velocidade final do carro é de , leste (inalterada).
- A velocidade final do carro é , a leste.
- A velocidade final do carro é de , a leste.