Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 8.Problemas - Ex. 69

As esferas A (massa 0,020   k g ), B (massa 0,030   k g ) e C (massa 0,050   k g ) se aproximam da origem deslizando sobre uma mesa de ar sem atrito (Figura 8.41 ). As velocidades iniciais de A e de B são indicadas na figura. Todas as três esferas atingem a origem no mesmo instante e ficam coladas. a) Quais devem ser os componentes x e y da velocidade inicial de C para que os três objetos unidos se desloquem a 0,50   m / s no sentido do eixo + O x   após a colisão? b) Se C possui a velocidade encontrada no item (a), qual é a variação da energia cinética do sistema das três esferas ocasionada pela colisão?

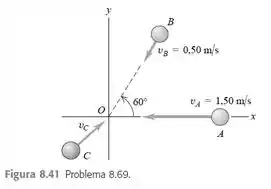
Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente encontrar (a) os componentes x e y da velocidade inicial de C para que os três objetos unidos se desloquem a 0,50   m / s no sentido do eixo + O x   após a colisão; e b) a variação da energia cinética do sistema das três esferas ocasionada pela colisão.

Os componentes x e y do momento do sistema são conservados. Após a colisão, as esferas estão juntas, logo a massa total após a colisão será:

m t o t a l = 0,100 k g

E se move com velocidade v 2 → , ok?

Sendo assim, vamos achar v C x e v C y para que v 2 → = ( 0,5 m / s ) i ^ .

Antes, mais uns pequenos detalhes:

v B x = - 0,5 cos ⁡ 60 °   m / s

E

v B y = - 0,5 sen ⁡ 60 °   m / s

E a esfera A só possui velocidade em x :

v A x = ( - 1,5 m / s ) i ^

Então, vamos calcular o momento linear no eixo x e no eixo y para obter as componentes da velocidade, depois, vamos calcular a variação da energia cinética Δ K , onde K é dada pela fórmula K = m v 2 2 .

Vamos lá!

Passo 2

(a) Olhando para o eixo x , temos a seguinte conservação de momento linear:

P 1 x = P 2 x

O que nos dá:

m A v A x + m B v B x + m C v C x = m t o t a l v 2 x

Já que, antes da colisão, todas as esferas estavam separadas e, após a colisão, estão juntas.

Isso implica que:

v C x = m t o t a l v 2 x - m A v A x - m B v B x m C

v C x = 0,100 k g ⋅ 0,50 m s - 0,020 k g ⋅ - 1,50 m s - 0,030 k g ⋅ - 0,50 m s cos ⁡ 60 ° 0,050 k g

∴

v C x = 1,75 m / s

Passo 3

E, no eixo y , temos:

P 1 y = P 2 y

O que nos dá:

m A v A y + m B v B y + m C v C y = m t o t a l v 2 y

Isso implica que:

v C y = m t o t a l v 2 y - m A v A y - m B v B y m C

v C y = 0 - 0 - 0,030 k g ⋅ - 0,50 m s sen ⁡ 60 ° 0,050 k g

v C y = 0,030 k g ⋅ 0,50 m s sen ⁡ 60 ° 0,050 k g

v C y = 0,260 m / s

Passo 4

(b) Primeiro, precisamos calcular:

v C = v C x 2 + v C y 2

v C = 1,77 m / s

Além disso, temos que:

∆ K = K 2 - K 1

Onde K é a energia cinética, que é dada por K = m v 2 2 .

Sendo assim:

K 2 = 0,100 k g 2 ⋅ 0,50 m s 2 = 0,0125 J

E

K 1 = 0,020 k g 2 ⋅ 1,50 m s 2 + 0,030 2 ⋅ 0,50 m s 2 + 0,050 k g 2 ⋅ 1,77 m s 2

K 1 = 0,1046 J

Isso implica que:

∆ K = - 0,092 J

Como não há força externa, o momento do sistema é conservado. As forças que as esferas exercem uma sobre a outra (forças internas) realizam trabalho negativo durante a colisão e isso reduz a energia cinética do sistema, beleza?

Show! Conseguimos!

Valeu, galera! Até a próxima! 😉

Resposta

  1. v C x = 1,75   m / s

    v C y = 0,260 m / s

∆ K = - 0,092 J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 9-64, o bloco A (com uma massa de 1,6k g ) desliza em direção ao bloco B (com uma massa de 2,4k g ) ao longo de uma superfície sem atrito. Os sentidos de três velocidades antes ( i ) e depois
Duas esferas de titânio se aproximam com a mesma velocidade escalar e sofrem uma colisão elástica frontal. Após a colisão, uma das esferas, cuja massa é 300g , permanece em repouso. (a) Qual é a massa
Na Fig. 9-69, o disco 1, de massa m 1=0,20k g , desliza sem atrito em uma bancada de laboratório até sofrer uma colisão unidimensional com o disco 2, inicialmente em repouso. O disco 2 é arremessado p
Um corpo com 2,0k g de massa sofre uma colisão elástica com um corpo em repouso e continua a se mover na mesma direção e sentido, mas com um quarto da velocidade inicial. (a) Qual é a massa do outro c
Na Fig. 9-66, a partícula 1, de massa m 1=0,30k g , desliza para a direita ao longo de um eixo x em um piso sem atrito com uma velocidade escalar de 2,0m / s . Quando chega ao ponto x=0 , sofre uma co