Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.11 - Ex. 55

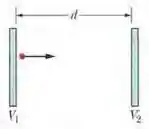
Na figura abaixo, uma partícula carregada (um elétron ou um próton) está se movendo para a direita entre duas placas paralelas carregadas separadas por uma distância d = 2,00   m m . Os potenciais das placas são V 1 = - 70,0   V e V 2 = - 50,0   V . A partícula partiu da placa da esquerda com uma velocidade inicial de 90,0   k m / s , mas a velocidade está diminuindo.

(a) A partícula é um elétron ou um próton?

(b) Qual é a velocidade da partícula ao chegar à placa 2?

Passo 1

Fala api, pessoal! 😁

Nesse problema temos uma partícula que se move para a direita entre duas placas, de V 1 para V 2 . A partícula tem velocidade inicial v 0 = 90 k m / s porém diminui ao longo do tempo.

Se V 1 = - 70 V e V 2 = - 50 V , queremos saber se a partícula é um eletron ou um proton e tambem qual é a velocidade da partícula ao chegar na placa 2.

Parece complicado? 🤔

Para sabermos se a partícula tem sinal positivo ou negativo, temos que usar as informações do comportamento da partícula e da diferença de potencial entre as placas em relação ao campo elétrico...

Agora para determinar a velocidade da partícula ao chegar em V 2 temos que relacionar o trabalho da força elétrica e a energia cinética do sistema...

Veja só! 👀

Passo 2

Na letra (a), o campo elétrico aponta para onde o potencial diminui. O potencial diminui para a esquerda. Então o campo elétrico aponta para a esquerda. Além disso, a força elétrica também é para a esquerda, já que a partícula está desacelerando.

Como a força elétrica e o campo elétrico têm o mesmo sentido, a carga tem que ser positiva, ou seja, é um próton.

Legal, né? 😁

Passo 3

Na letra (b), para achar a velocidade da partícula, vamos lembrar que o trabalho da força resultante é igual à variação da energia cinética.

W f o r ç a   e l é t r i c a = Δ E c

Mas lembre se que o trabalho da força elétrica é dado por:

W = q U = q ( V i - V f )

U é a diferença de potencial. Aí fica assim:

q U = m v f 2 2 - m v i 2 2

2 q U m = v f 2 - v i 2

Simplificando...

2 q ( V i - V f ) m = v f 2 - v i 2

v f = v i 2 + 2 q ( V i - V f ) m

Substituindo os valores, obtemos:

v f = 90 × 10 3   m / s 2 + 2 ( 1,60 × 10 - 19   C ) ( - 70   V - ( - 50   V ) ) 1,67 × 10 - 27   k g

v f = 6,53 × 10 4   m / s = 65,3   k m / s

E aí! O que achou? Responde Aí! 😎

Resposta

Letra (a): Próton

Letra (b): 65,3   k m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reproduza a FIGURA Q29.14 sobre uma folha de papel. Depois desenhe um ponto (ou vários pontos) sobre a figura para indicar a posição (ou posições) em que o potencial elétrico é nulo.
Um dipolo elétrico possui momento de dipolo p. Para r ≫ s , onde s é a separação entre as cargas, mostre que o potencial elétrico do dipolo pode ser escrito como V = 1 4 π ε 0 ⋅ p c o s θ r 2 onde r é
O arranjo de cargas mostrado na FIGURA P29.68 é chamado de quadripolo elétrico linear. As cargas positivas estão localizadas em y = ± s . Note que a carga total do quadripolo é nula. Obtenha uma expre
Uma carga de 1,0 nC encontra-se na origem de um sistema de coordenadas. Uma carga de - 3 u C encontra-se sobre o eixo x em x = 4,0 c m . Encontre todos os pontos do plano xy nos quais o potencial é nu
Um próton é lançado, de longe, em direção ao núcleo de um átomo de ferro. O ferro é o elemento de número atômico 26 e o diâmetro de seu núcleo é de 9,0 fm. Qual deve ser a velocidade inicial do próton