Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 25.5 - Ex. 36
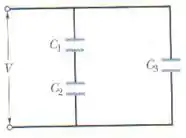
Na figura, uma diferença de potencial V = 100 V é aplicada a um circuito de capacitores cujas capacitâncias são = 10,0 μF, = 5,00 μF e = 4,00 μF. Determine (a) ; (b) ; (c) a energia armazenada ; (d) ; (e) ; (f) ; (g) ; (h) ; (i) .
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Este é um problema complexo no qual temos capacitores em paralelo e em série. Nos são fornecidos a capacitância e a voltagem de cada capacitor. Precisamos encontrar a carga , a voltagem e a energia armazenada para cada capacitor. Vamos usar a seguinte equa��ão para carga e voltagem:
Isso ocorre porque a carga aumenta quando a voltagem aumenta. A voltagem pode ser calculada a partir da equação (1) expressando-a da seguinte forma:
E, por fim, precisamos lembrar da equação para a energia armazenada:
Você se lembra das equações para capacitores em série e em paralelo?
Passo 2
Parabéns se você se lembrou. A equação para capacitores em paralelo é:
E para capacitores em série:
Usaremos ambas essas equações para continuar a resolução.
Nesta parte, precisamos apenas calcular a terceira carga. A capacitância do terceiro capacitor é fornecida, mas e a voltagem? Bem, a voltagem é a mesma que a voltagem total, como podemos ver na imagem. Usando a primeira equação, obtemos:
Este é o valor da carga no terceiro capacitor que vamos usar para cálculos adicionais.
Passo 3
b) Como já mencionado no passo anterior, a voltagem no terceiro capacitor é a mesma que a voltagem total. Dito isso, o valor é:
Você consegue calcular a energia armazenada para o terceiro capacitor? Com o que a energia armazenada está relacionada?
Passo 4
c) Vamos lembrar o que dissemos no início. A equação da energia armazenada (3) está relacionada à capacitância e à voltagem. Agora, esta é a , o que significa que, a partir da fórmula, precisamos de e . No passo anterior, encontramos o valor da voltagem, e o valor da capacitância nos foi dado. Podemos usar nossa equação para resolver este problema.
Essa é a nossa energia armazenada para o terceiro capacitor.
Passo 5
d) Para calcular o valor da carga no primeiro e segundo capacitor, precisaremos encontrar a capacitância equivalente para os dois capacitores dados. Eles estão em série, o que significa que a equação para a carga será a seguinte:
Substituindo os valores dados:
esse é o valor da carga .
Passo 6
e) Lembre-se da equação (2) para que possamos resolver a voltagem do segundo capacitor. A voltagem no primeiro capacitor será igual a:
usaremos esse valor para determinar e também algo mais tarde. Você se lembra do que é esse "algo mais"?
Passo 7
f) Da mesma forma que fizemos na parte c), completaremos essa solução diretamente usando a equação para energia armazenada, pois temos todas as informações necessárias. Essa era a outra coisa em que você precisa usar o valor para a voltagem . Cálculo:
Outra equação simples e cálculo.
Passo 8
Para calcular o valor da carga nos capacitores 1 e 2, precisaremos encontrar a capacitância equivalente para esses dois capacitores fornecidos. Eles estão em série, o que significa que a equação para a carga será a seguinte:
Substituindo os valores dados:
esse é o valor da carga .
g) A carga é a mesma que , o que significa:
Passo 9
h) Agora, o que devemos fazer com a voltagem? Temos a voltagem total, bem como a voltagem . Na série, a voltagem total é a soma de todas as voltagens, o que significa:
A partir daqui, podemos expressar a diferença de potencial e calculá-la usando os valores dos passos anteriores:
i) Por fim, precisamos encontrar a energia armazenada , o que pode ser feito novamente usando a mesma equação que usamos para o problema anterior com a energia armazenada.
E este é o fim desta solução.
Resposta
Letra (a):
Letra (b):
Letra (c):
Letra (d):
Letra (e):
Letra (f):
Letra (g):
Letra (h):
Letra (i):