Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 25.4 - Ex. 26
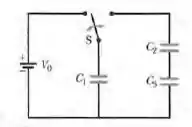
A Fig. abaixo mostra uma bateria de e três capacitares descarregados de capacitâncias , e . A chave é deslocada para a esquerda até que o capacitar esteja totalmente carregado. Em seguida, a chave é deslocada para a direita. Determine a carga final (a) do capacitor ; (b) do capacitor ; (c) do capacitor .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Na figura, temos uma bateria de e três capacitores descarregados com as seguintes capacitâncias: , e .
A chave é deslocada para a esquerda até que o capacitor 1 esteja totalmente carregado. Em seguida, a chave é deslocada para a direita.
Agora, vamos determinar a carga final para cada um dos capacitores:
Carga final do capacitor 1 (a):
Quando a chave é deslocada para a esquerda, o capacitor 1 começa a carregar. A carga final no capacitor 1 será igual à carga total fornecida pela bateria.
Carga final do capacitor 2 (b) e a carga final do capacitor 3 (c):
Os capacitores 2 e 3 não está conectado diretamente à bateria, mas a carga total fornecida pela bateria é distribuída entre os três capacitores. Portanto, a carga final nos capacitores 2 e 3 também será afetada.
Em resumo, a carga final em cada capacitor dependerá da distribuição de carga durante o processo de carregamento e descarregamento.
Veja só! 😉
Passo 2
Bem, os capacitores 2 e 3 estão em série e podem ser substituídos por um capacitor com capacitância igual a:
A carga do capacitor equivalente (chamaremos de é a mesma carga do capacitor 2 e 3, pois eles estão em série. Chamaremos as cargas do capacitor 2 e 3 de e . Então, .
A diferença de potencial entre os terminais do capacitor equivalente é
A diferença de potencial entre as placas do capacitor 1 é . Como a diferença de potencial entre as placas do capacitor equivalente é a mesma das placas do capacitor 1, pois eles estão em paralelo, então,
Quando a gente muda a chave para a direita, parte da energia do capacitor 1 vai para os capacitores 2 e 3. Vamos chamar de a carga inicial do capacitor 1, de acordo com a lei de conservação de energia, em que é a diferença de potencial original do capacitor 1.
Tranquilo até aqui? 😬
Passo 3
Item (a)
Precisamos resolver o sistema de equações encontrados nos passos anteriores:
Simplificando...
Substituindo pelos valores que temos no enunciado, obtemos
Tranquilo até aqui? 😁
Passo 4
Item (b)
Como dito anteriormente
Sabemos então que
Item (c)
Como a carga do capacitor 2 é igual a carga do capacitor 3, já que eles estão em série,
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
