Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.Problemas Adicionais - Ex. 69
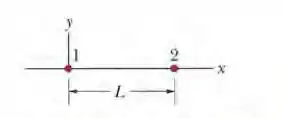
Na Fig. abaixo, a partícula 1, de carga -5,00q, e a partícula 2, de carga + 2,00q, são mantidas a uma distância L no eixo x. Se uma partícula 3, de carga desconhecida , é colocada em um ponto tal que a força eletrostática total exercida sobre a partícula é zero, determine (a) a coordenada x; (b) a coordenada y da partícula 3.
Passo 1
O enunciado fala de uma partícula de carga que deve ser inserida em uma posição tal que a força eletrostática resultante das partículas 1 e 2 seja nula. Como as partículas 1 e 2 estão no eixo x, é conveniente que a partícula 3 também esteja no eixo x, iremos discutir isso melhor no item (b). Vamos pensar em qual região essa partícula deve ser inserida: como as partículas 1 e 2 tem sinais opostos, a partícula 3 não pode ser inserida entre elas já que nessa região as forças exercidas por cada partícula terão o mesmo sentido. Portanto a partícula terá que ficar à esquerda da partícula 1 ou à direita da partícula 2. Como a carga da partícula 1 é maior em módulo, a partícula deve estar mais longe dela pra que a soma vetorial das forças seja nula. Então, a partícula deve ficar à direita da partícula 2.
Passo 2
Faremos o calculo da soma das forças. A força eletrostática é dada pela Lei de Coulomb:
A força resultante na partícula 3 é . Sendo a distância entre a partícula 3 e a partícula 2, então a distância entre a partícula 3 e a partícula 1 é de . A força resultante na partícula 3 será:
Como o enunciado pede a distância para que a força total seja igual a zero, então:
Passo 3
Item (a)
Para achar a coordenada basta isolá-la na equação acima:
Resolvendo essa equação de 2° grau, obtemos:
Como sabemos, procuramos a distância à direita da partícula 2, portanto devemos usar o sinal positivo. Se utilizarmos o sinal negativo a distância será no meio entre as duas partícula, o que já discutimos que é improvável Então,
Passo 4
Item (b)
A coordenada y tem que ser igual a zero, pois para que a soma dos dois vetores seja nula, necessariamente a carga tem que está no mesmo eixo das duas cargas 1 e 2.