Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.7 - Ex. 37

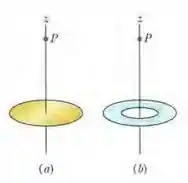
Um engenheiro foi encarregado de projetar um dispositivo no qual um disco uniformemente carregado de raio R produz um campo elétrico. O módulo do campo é mais importante em um ponto P sobre o eixo do disco, a uma distância 2,00 R do plano do disco (figura a). Para economizar material, decidiu-se substituir o disco por um anel com o mesmo raio externo R e um raio interno R / 2,00 (figura b). O anel tem a mesma densidade superficial de cargas que o disco original. Qual é a redução percentual do módulo do campo elétrico no ponto P?

Passo 1

Fala aí! tudo certinho? 😁

A questão quer saber da gente qual vai ser a redução percentual do campo elétrico no ponto P se trocarmos a configuração do disco pro anel ali.

Primeiro, meu jovem, vamos à fórmula do campo gerado por um disco carregado uniformemente:

E = σ 2 ϵ 0 1 - z z 2 + R 2

Mas cuidado! Essa equação é só para pontos que estejam no eixo que passa pelo centro do disco, ok? Esse resultado está deduzido na página 33 😉. Para calcular o campo em (a), a gente só precisa fazer z = 2 R :

E a = σ 2 ϵ 0 1 - 2 R 4 R 2 + R 2

A partir dessa equação vamos encontrar a equação pro anel e relacioná-las, beleza?bora lá! 😉

Passo 2

Agora que vem o pulo do gato. Para calcular o campo em b , a ideia é essa aqui oh: a gente tem que pegar um disco igualzinho ao de “a”, só que a gente agora vai sobrepor um disco menor, de raio R / 2 , com carga oposta. Pode isso, Arnaldo? Pode, pelo Princípio da Superposição. Aí fica assim:

E b = E a - σ 2 ϵ 0 1 - 2 R 4 R 2 + ( R / 2 ) 2

E a - E b = σ 2 ϵ 0 1 - 2 R 4 R 2 + ( R / 2 ) 2

Beleza, encontramos aqui a equação pra nova configuração de anel, somente retirando um disco menor do disco maior.

Veja só! 👀

Passo 3

Agora só falta calcular a diferença percentual. E o que é isso? É a diferença dividida pelo valor anterior, ou seja, queremos isso:

E a - E b E a  

Só que já sabemos o numerador e o denominador, aí fica essa coisinha linda:

E a - E b E a = σ 2 ϵ 0 1 - 2 R 4 R 2 + ( R / 2 ) 2 σ 2 ϵ 0 1 - 2 R 4 R 2 + R 2

Agora é a melhor parte, é só cortar tudão e substituir os valores de R = 1 m :

E a - E b E a = 1 - 2 4 + 1 / 4 1 - 2 4 + 1 = 0,0299 0,1056 = 0,283 ≈ 28 %

E aí! entendeu tudo? Responde Aí! 😊

Resposta

E a - E b E a ≈ 28 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. Abaixo mostra dois anéis concêntricos, de raios R e R' = 3,00R, que estão no mesmo plano. O ponto P está no eixo central z, a uma distância D = 2,00R do centro dos anéis. O anel menor possui um
A Fig. 22-43 mostra dois anéis não condutores paralelos, com o centro na mesma reta perpendicular aos planos dos anéis. O anel 1, de raio R , possui uma carga uniforme q 1 ; o anel 2, também de raio R
Na Fig. 22-46, uma barra não condutora de comprimento L = 8,15c m tem uma carga - q = - 4,23f C uniformemente distribuída. (a) Qual é a densidade linear de cargas da barra? Determine (b) o módulo e (c
Na Fig. 22-44, uma barra fina de vidro forma uma semicircunferência de raio r = 5,00c m . Uma carga + q = 4,50p C está distribuída uniformemente na parte superior da barra e uma carga - q = - 4,50p C
Uma barra fina não condutora, com uma distribuição uniforme de carga positiva Q , tem a forma de uma circunferência de raio R fig. 22-49. O eixo central do anel é o eixo z , com a origem no centro do