Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 36.Exercícios e Problemas - Ex. 17
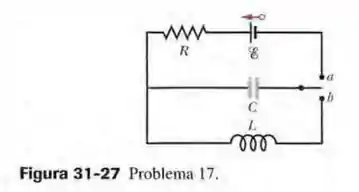
Na Fig. 31-27, a fonte ideal tem uma força eletromotriz . A chave é mantida na posiçāo por um longo tempo e depois é colocada na posiçāo . Determine (a) a frequência e (b) a amplitude das oscilações resultantes.
Passo 1
E aí galerinha, vamos destruir essa questão comigo? Vamos láaaa!
(a) Quando a chave é colocada na posição , o circuito se torna um circuito . Assim, a frequência angular de oscilação é́ e a frequência é
Passo 2
(b) Como a chave permaneceu muito tempo na posição , o capacitor se carregou totalmente. Assim, quando a chave é colocada na posição , a tensão entre as placas do capacitor é e a carga do capacitor é . A amplitude da corrente é
Opa, gostou da resolução? Responde Aí!
Resposta
a.
b.
Exercícios de Livros Relacionados
PLANILHA ELETRONICA Usando uma planilha eletrônica faca um grafico de V.versus a frequencia de entrada f e um grafico do angulo de fase 8 versus a frequencia de entrada para o filtro passa-baixas dos
A Figura 29-41 mostra um indutor em serie com um capacitor de placas paralelas.O capacitor tem largura to de 20 cme espacamento de 2,0 mm.Um dieletrico com constante dieletrica de 4,8 pode deslizar pa
1 . Você possui uma lâmpada especial com um filamento muito delicado. O fio se romperá se a corrente fluindo por ele ultrapassar 1,50A , mesmo que por um instante. Qual é a maior corrente quadrática m
15 . O resistor, o indutor, o capacitor e a fonte de tensão do Exercício 31.14 são conectados formando um circuitoL - R - C em série. ( a ) Qual é a impedância do circuito? ( b ) Qual é a amplitude da
16 . Você dispõe de um resistor de 200V , de um indutor de 0,900H , de um capacitor de 6,00μ F e uma fonte de tensão com amplitude de tensão de 30,0V e frequência angular de 250r a d / s , todos conec