Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.11 - Ex. 56
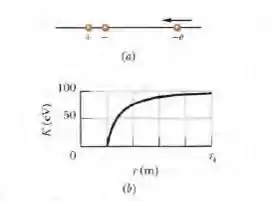
A Fig. (a) mostra um elétron que se move ao longo do eixo de um dipolo elétrico em direção ao lado negativo do dipolo. O dipolo é mantido fixo no lugar. O elétron estava inicialmente a uma distância muito grande do dipolo, com uma energia cinética de . A Fig. (b) mostra a energia cinética K do elétron em função da distância em relação ao centro do dipolo. A escala do eixo horizontal é definida por . Qual é o módulo do momento do dipolo?
Passo 1
Para essa questão, precisamos lembrar que , sendo o potencial de uma carga, a carga e o potencial elétrico dessa carga. Você lembra também a fórmula do potencial de um dipolo? É esse:
Sendo é o módulo do momento dipolar e é o ângulo entre o eixo do dipolo e o ponto em que queremos calcular o mesmo.
Com essas duas fórmulas podemos calcular o potencial elétrico do elétron, dessa forma :
De acordo com a figura (b), a energia potencial do elétron no ponto em que o é menor, isto é, maior aproximação do dipolo (, chamaremos de que é o ponto final, é:
Em que
Passo 2
Como o elétron parte de uma distância muito grande do elétron, o potencial inicialmente era zero, isto é, Lembre-se que o ponto que escolhemos como ponto final, tem energia cinética zero, portanto, . Através da conservação da energia, podemos concluir, então, que .
Passo 3
Assim,